��Ŀ����
����Ŀ��2016��9�£�ij�ֻ���˾�������¿������ֻ���Ϊ�˵���ijС��ҵ���Ըÿ��ֻ��Ĺ������ù�˾��ijС������Բ���ҵ���������ʾ����飬�涨ÿ��ֻ�ܴ�A�ࣨ����ȥ��������B�ࣨ���ۺ���ȥ��C�ࣨ��ԥ�У���D�ࣨ�϶�������������ѡһ�࣬���Ƴ�������������������ͳ��ͼ����ͼ������������Ϣ����������⣺
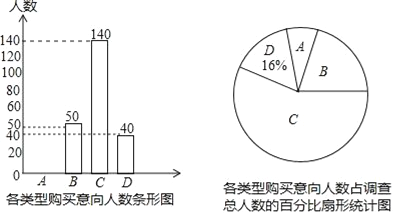
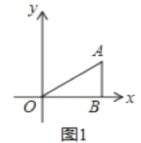
��1������ͳ��ͼ��B���Ӧ�İٷֱ�Ϊ�� ��%���벹ȫ����ͳ��ͼ��
��2������С������4000�ˣ�������Ƹ�С����Լ�ж���������ȥ�����ÿ��ֻ���
���𰸡���1��20����ͼ����������2�����Ƹ�С����Լ��320������ȥ�����ÿ��ֻ���
�������������������1��������������ټ���B���Ӧ�İٷֱȣ���������ͼ���ɣ�
��2�����������������˼�뼴�������.
�����������1������D��İٷֱ��Լ���������֪������=40��16%=250���ˣ�������ͳ��ͼ��B���Ӧ�İٷֱ�Ϊ![]() ��A������=250��50��140��40=20��
��A������=250��50��140��40=20��
��ȫ����ͳ��ͼ���£�
��2�����Ƹ�С������ȥ�����ÿ��ֻ�����A��ѡ�����4000��![]() %=320���ˣ�
%=320���ˣ�
�𣺹��Ƹ�С����Լ��320������ȥ�����ÿ��ֻ���

 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�����Ŀ���������˻��״Ӻ���![]() ����������
����������![]() ����Ǧֱ���������ͬʱ���������˻��ҴӺ���
����Ǧֱ���������ͬʱ���������˻��ҴӺ���![]() ����������
����������![]() ����Ǧֱ�����������˻�����ʱ��Ϊ
����Ǧֱ�����������˻�����ʱ��Ϊ![]() �����˻��ס�������λ�õĸ߶ȷֱ�Ϊ
�����˻��ס�������λ�õĸ߶ȷֱ�Ϊ![]() ��
��![]()
��1���������⣬��д�±���
����ʱ�� | 5 | 10 |
|
| 25 |
| |
| 60 |
|
��2������ֱ�д��![]() ��
��![]() ��
��![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��3����ijʱ���������˻��ܷ�λ��ͬһ�߶ȣ����ܣ������˻�������ʱ������ڸ߶ȣ������ܣ���˵�����ɣ�
����Ŀ�����ŵ������������ķ�չ��������![]() �������ѳ�Ϊ�ܶ�������е�ѡ�����ѧԺ·վ�������ȳ���������������ҽϽ���
�������ѳ�Ϊ�ܶ�������е�ѡ�����ѧԺ·վ�������ȳ���������������ҽϽ���![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �е�ijһվ�����������ﹲ�������ؼң�������������վ����ѧԺ·����Ϊ
�е�ijһվ�����������ﹲ�������ؼң�������������վ����ѧԺ·����Ϊ![]() ����λ��ǧ�ף�������������ʱ��
����λ��ǧ�ף�������������ʱ��![]() (��λ������)�ǹ���
(��λ������)�ǹ���![]() ��һ�κ��������ϵ���±���
��һ�κ��������ϵ���±���
����վ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
��![]() ����
����![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��![]() ����ﵥ����ʱ��
����ﵥ����ʱ��![]() (��λ������)��
(��λ������)��![]() �Ĺ�ϵʽΪ
�Ĺ�ϵʽΪ![]() �������ѧԺ·վ�ص��ҵ������ʱ�䣬��ָ��������һվ��������
�������ѧԺ·վ�ص��ҵ������ʱ�䣬��ָ��������һվ��������