Question

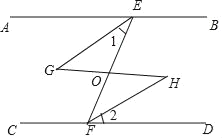
【题目】已知：如图，点E、F分别在直线AB、CD上，点G、H在两直线之间，线段EF与GH相交于点O，且有∠AEF+∠CFE＝180°，∠AEF﹣∠1＝∠2，则在图中相等的角共有（　　）

A. 5对B. 6对C. 7对D. 8对

Answer 1

【答案】D

【解析】

依据∠AEF+∠CFE＝180°，即可得到AB∥CD，依据平行线的性质以及对顶角的性质，即可得到图中相等的角．

解：∵∠AEF+∠CFE＝180°，

∴AB∥CD，

∴∠AEF＝∠DFE，∠CFE＝∠BEF，

∵∠AEF﹣∠1＝∠2，∠AEF﹣∠1＝∠AEG，

∴∠AEG＝∠2，

∴∠1＝∠EFH，∠BEG＝∠CFH，

∴GE∥FH，

∴∠G＝∠H，

又∵∠EOG＝∠FOH，∠EOH＝∠GOF，

∴图中相等的角共有8对，

故选：D．