题目内容
【题目】如图，点M、N分别是正方形ABCD的边CD、CB上的动点，满足DM=CN，AM与DN相交于点E，连接CE，若正方形的边长为2，则线段CE的最小值是______________．
【答案】
-1
【解析】
根据题意可得△DCN≌△ADM，可得∠CDN＝∠DAM，可证∠DEA＝90°，则点E是以AD为直径的圆上一点，则可得不等式，可解得线段CE的最小值．
取AD中点O，连接OE，OC
∵ABCD是正方形
∴AD＝CD，∠ADC＝∠DCB＝90°且DM＝CN
∴△ADM≌△DCN
∴∠CDN＝∠DAM
∵∠CDN＋∠ADN＝90°
∴∠DAM＋∠ADN＝90°
∴∠AED＝90°
∴点E是以AD为直径的圆上一点，
如图所示
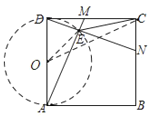
∵正方形ABCD的边长为2，O是AD中点
∴CD＝2，OD＝1＝OE
∴OC＝
=
∵EC≥OCOE＝1
∴EC的最小值为1
故答案为1．
练习册系列答案
相关题目
