��Ŀ����
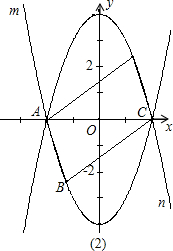
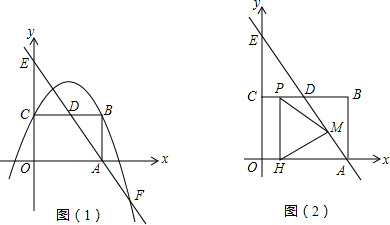
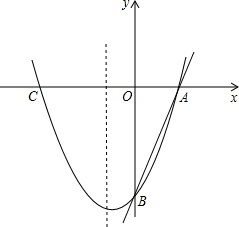
��ͼ����֪������m�Ľ���ʽΪy=x2-4����x�ύ��A��C���㣬B��������m�ϵĶ��㣨B����A��C�غϣ�����B��x����·���������n��������m����x��Գƣ���ACΪ�Խ��ߵ�ƽ���ı���ABCD�ĵ��ĸ�����ΪD��
��1����֤����Dһ����������n�ϣ�
��2��ƽ���ı���ABCD�ܷ�Ϊ���Σ�����Ϊ���Σ������Щ���ι������ֵ��������ֻ��һ�����η�������������˾��ε��������������Ϊ���Σ���˵�����ɣ�
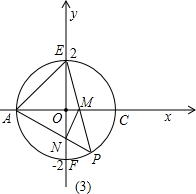
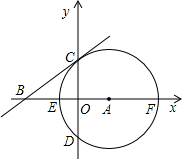
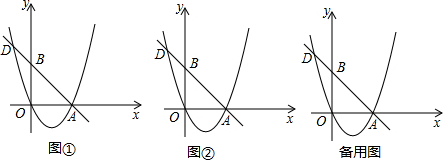
��3������2���й�A��B��C��D��Բ��y����E��F����P�ǻ�CF��һ���㣨������C��F���㣩������AP��y����N������EP��x����M����P���˶�ʱ���ı���AEMN������Ƿ�ı䣿�����䣬��������������仯����˵�����ɣ�

��1����֤����Dһ����������n�ϣ�
��2��ƽ���ı���ABCD�ܷ�Ϊ���Σ�����Ϊ���Σ������Щ���ι������ֵ��������ֻ��һ�����η�������������˾��ε��������������Ϊ���Σ���˵�����ɣ�
��3������2���й�A��B��C��D��Բ��y����E��F����P�ǻ�CF��һ���㣨������C��F���㣩������AP��y����N������EP��x����M����P���˶�ʱ���ı���AEMN������Ƿ�ı䣿�����䣬��������������仯����˵�����ɣ�



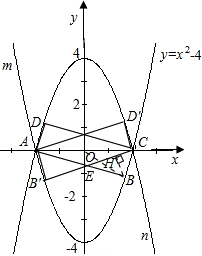
��1��֤������n�Ľ���ʽΪy=ax2+bx+c��a��0����
��n��x��Ľ���ΪA��-2��0����C��2��0�������������ǣ�0��-4����m��n����x��Գƣ�
��m��A��-2��0����C��2��0�������������ǣ�0��4����
��
��a=-1��b=0��c=4��
��n�Ľ���ʽΪy=-x2+4��
���B��m��n��Ϊm��y=x2-4������һ�㣬��n=m2-4��
���ı���ABCD��ƽ���ı��Σ���A��C����ԭ��O�Գƣ�
��B��D����ԭ��O�Գƣ�
���D������ΪD��-m��-n����
��ʽ����ʽ��֪��-n=-��m2-4��=-��-m��2+4��
����D����������y=-x2+4��
���D��n�ϣ�
��2��?ABCD������
����B��BH��x����H���ɵ�B��m��y=x2-4�ϣ������B������Ϊ��x0��x02-4����
��OH=|x0|��BH=|x02-4|��
��֪�����ҽ���BO=AO=2ʱ��?ABCDΪ���Σ�
��Rt��OBH�У��ɹ��ɶ����ã�|x0|2+|x02-4|2=22��
��x02-4����x02-3��=0��
��x0=��2����ȥ����x0=��
����7�֣�
���ԣ�����B����ΪB��
��-1����B�䣨-
��-1��ʱ��?ABCDΪ���Σ�
��ʱ����D������ֱ���D��-
��1����D�䣨
��1����
��ˣ����������ľ�������ֻ��2����������ABCD�;���AB��CD�䣮
��3����ֱ��AB��y�ύ��E����Ȼ����AOE����AHB��
��
=
��
��
=
��
��EO=4-2
��
�ɸ�ͼ�εĶԳ���֪����ABCD�����AB��CD���غϲ��������Σ������Ϊ
S=2S��ACE=2��
��AC��EO=2��
��4����4-2
��=16-8
�����ı���AEMN��������ı䣬Ϊ16-8
��
��n��x��Ľ���ΪA��-2��0����C��2��0�������������ǣ�0��-4����m��n����x��Գƣ�
��m��A��-2��0����C��2��0�������������ǣ�0��4����
��
|
��a=-1��b=0��c=4��
��n�Ľ���ʽΪy=-x2+4��
���B��m��n��Ϊm��y=x2-4������һ�㣬��n=m2-4��
���ı���ABCD��ƽ���ı��Σ���A��C����ԭ��O�Գƣ�
��B��D����ԭ��O�Գƣ�
���D������ΪD��-m��-n����
��ʽ����ʽ��֪��-n=-��m2-4��=-��-m��2+4��
����D����������y=-x2+4��
���D��n�ϣ�
��2��?ABCD������
����B��BH��x����H���ɵ�B��m��y=x2-4�ϣ������B������Ϊ��x0��x02-4����
��OH=|x0|��BH=|x02-4|��
��֪�����ҽ���BO=AO=2ʱ��?ABCDΪ���Σ�
��Rt��OBH�У��ɹ��ɶ����ã�|x0|2+|x02-4|2=22��
��x02-4����x02-3��=0��
��x0=��2����ȥ����x0=��
| 3 |
���ԣ�����B����ΪB��
| 3 |
| 3 |
��ʱ����D������ֱ���D��-
| 3 |
| 3 |
��ˣ����������ľ�������ֻ��2����������ABCD�;���AB��CD�䣮
��3����ֱ��AB��y�ύ��E����Ȼ����AOE����AHB��
��
| EO |
| AO |
| BH |
| AH |
��
| EO |
| 2 |
| 1 | ||
2+
|
��EO=4-2
| 3 |
�ɸ�ͼ�εĶԳ���֪����ABCD�����AB��CD���غϲ��������Σ������Ϊ
S=2S��ACE=2��
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |


��ϰ��ϵ�д�
�����Ŀ
 D���㣬��C������A������BC��x����B��
D���㣬��C������A������BC��x����B��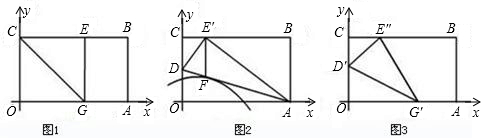
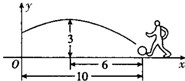
 ����ƽ��1����λ���Ⱥ�á�AA1B1��
����ƽ��1����λ���Ⱥ�á�AA1B1��