Question

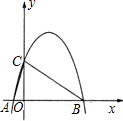
如图，Rt△OAB中，∠OAB=90°，O为坐标原点，边OA在x轴上，OA=AB=1个单位长度，把Rt△OAB沿x轴正方向平移1个单位长度后得△AA₁B₁．
（1）求以A为顶点，且经过点B₁的抛物线的解析式；
（2）若（1）中的抛物线与OB交于点C，与y轴交于点D，求点D、C的坐标．

Answer 1

（1）由题意可知，A（1，0），A₁（2，0），B₁（2，1），
设以A为顶点的抛物线的解析式为y=a（x-1）²；
∵此抛物线过点B₁（2，1），
∴1=a（2-1）²，
∴a=1，
∴抛物线的解析式为y=（x-1）²；

（2）∵当x=0时，y=（0-1）²=1，
∴D点坐标为（0，1），
由题意得OB在第一象限的角平分线上，
故可设C（m，m），
代入y=（x-1）²；得m=（m-1）²；
解得m₁=

3- 5

2

＜1，m₂=

3+ 5

2

＞1（舍去）．
故C点坐标为（

3- 5

2

，

3- 5

2

）．