题目内容
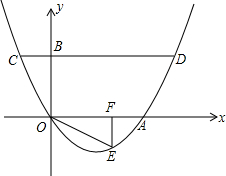
OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.
(1)如图1,在OA上选取一点G,将△COG沿CG翻折,使点O落在BC边上,记为E,求折痕y1所在直线的解析式;
(2)如图2,在OC上选取一点D,将△AOD沿AD翻折,使点O落在BC边上,记为E'.
①求折痕AD所在直线的解析式;
②再作E'F∥AB,交AD于点F.若抛物线y=-
x2+h过点F,求此抛物线的解析式,并判断它与直线AD的交点的个数.
(3)如图3,一般地,在OC、OA上选取适当的点D'、G',使纸片沿D'G'翻折后,点O落在BC边上,记为E''.请你猜想:折痕D'G'所在直线与②中的抛物线会有什么关系?用(1)中的情形验证你的猜想.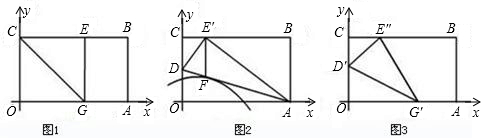
(1)如图1,在OA上选取一点G,将△COG沿CG翻折,使点O落在BC边上,记为E,求折痕y1所在直线的解析式;
(2)如图2,在OC上选取一点D,将△AOD沿AD翻折,使点O落在BC边上,记为E'.
①求折痕AD所在直线的解析式;
②再作E'F∥AB,交AD于点F.若抛物线y=-
| 1 |
| 12 |
(3)如图3,一般地,在OC、OA上选取适当的点D'、G',使纸片沿D'G'翻折后,点O落在BC边上,记为E''.请你猜想:折痕D'G'所在直线与②中的抛物线会有什么关系?用(1)中的情形验证你的猜想.

(1)由折叠法知,四边形OCEG是正方形,
∴OG=OC=6,
∴G(6,0),C(0,6).
设直线CG的解析式为y=kx+b,
则0=6k+b,6=0+b,
∴k=-1,b=6,
∴直线CG的解析式为:y=-x+6.
(2)①在Rt△ABE'中,BE'=
=8,
∴CE′=2.
设OD=s,则DE'=s,CD=6-s,
在Rt△DCE'中,s2=(6-s)2+22,
∴s=
.
则D(0,
)
设AD:y=k'x+
,
由于它过A(10,0),
∴k'=-
,
∴AD:y=-
x+
.
②∵E'F∥AB,E'(2,6),
∴设F(2,yF),
∵F在AD上,
∴yF=-
×2+
=
,
∴F(2,
).
又∵点F在抛物线y=-
x2+h上,
∴
=-
×4+h,
∴h=3.
∴抛物线的解析式为:y=-
x2+3.
即-
x2+
x-
=0,
∵△=(
)2-4×(-
)×(-
)=0
∴直线AD与抛物线只有一个交点.
(3)例如可以猜想:
(ⅰ)折痕所在直线与抛物线y=-
x2+3只有一个交点;
或(ⅱ)若作E''F''∥AB,交D'G'于F',则F'在抛物线y=-
x2+3上.
验证:(ⅰ)在图1中,折痕为CG,
将y=-x+6代入y=-
x2+3,
得-
x2+x-3=0.
∵△=1-4×(-3)×(-
)=0,
∴折痕CG所在直线的确与抛物线y=-
x2+3只有一个交点.
或(ⅱ)在图1中,D'即C,E''即E,G'即G,交点F'也为G(6,0),
∴当x=6时,y=-
x2+3=-
×62+3=0,
∴G点在这条抛物线上.
∴OG=OC=6,
∴G(6,0),C(0,6).
设直线CG的解析式为y=kx+b,
则0=6k+b,6=0+b,
∴k=-1,b=6,
∴直线CG的解析式为:y=-x+6.
(2)①在Rt△ABE'中,BE'=
| 102-62 |
∴CE′=2.
设OD=s,则DE'=s,CD=6-s,
在Rt△DCE'中,s2=(6-s)2+22,
∴s=
| 10 |
| 3 |
则D(0,
| 10 |
| 3 |
设AD:y=k'x+
| 10 |
| 3 |
由于它过A(10,0),
∴k'=-
| 1 |
| 3 |
∴AD:y=-
| 1 |
| 3 |
| 10 |
| 3 |
②∵E'F∥AB,E'(2,6),
∴设F(2,yF),
∵F在AD上,
∴yF=-
| 1 |
| 3 |
| 10 |
| 3 |
| 8 |
| 3 |
∴F(2,
| 8 |
| 3 |
又∵点F在抛物线y=-
| 1 |
| 12 |
∴
| 8 |
| 3 |
| 1 |
| 12 |
∴h=3.
∴抛物线的解析式为:y=-
| 1 |
| 12 |
即-
| 1 |
| 12 |
| 1 |
| 3 |
| 1 |
| 3 |
∵△=(
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 3 |
∴直线AD与抛物线只有一个交点.
(3)例如可以猜想:
(ⅰ)折痕所在直线与抛物线y=-
| 1 |
| 12 |
或(ⅱ)若作E''F''∥AB,交D'G'于F',则F'在抛物线y=-
| 1 |
| 12 |
验证:(ⅰ)在图1中,折痕为CG,
将y=-x+6代入y=-
| 1 |
| 12 |
得-
| 1 |
| 12 |
∵△=1-4×(-3)×(-
| 1 |
| 12 |
∴折痕CG所在直线的确与抛物线y=-
| 1 |
| 12 |
或(ⅱ)在图1中,D'即C,E''即E,G'即G,交点F'也为G(6,0),
∴当x=6时,y=-
| 1 |
| 12 |
| 1 |
| 12 |
∴G点在这条抛物线上.

练习册系列答案
相关题目




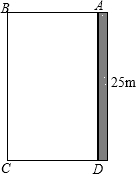 带一边靠墙,另三边用总长为40m的栅栏围住(如图4).若设绿化带的BC边长为xm,绿化带的面积为ym2.
带一边靠墙,另三边用总长为40m的栅栏围住(如图4).若设绿化带的BC边长为xm,绿化带的面积为ym2.