题目内容
如图,在边长为2个单位长度的正方形ABCD中,点O、E分别是AD、AB的中点,点F是以点O为圆心,OE长为半径的圆弧与DC的交点,点P是
上的动点,连接OP并延长交直线BC于K.
(1)当P从E点沿
运动到F时,K运动了多少单位长度?
(2)过点P作
所在圆的切线,当该切线不与BC平行时,设它与射线AB、直线BC分别交于M、G,
①当K与B重合时,BG:BM=?
②在P运动过程中,是否存在BG:BM=3的情况?若存在,求出BK的值;若不存在说明理由.

 |
| EF |
(1)当P从E点沿
 |
| EF |
(2)过点P作
 |
| EF |
①当K与B重合时,BG:BM=?
②在P运动过程中,是否存在BG:BM=3的情况?若存在,求出BK的值;若不存在说明理由.

(1)连接OE、OF,并延长OE、OF分别交直线BC于N、Q,
当P从点E运动到点F时,点K从点N运动到了点Q;
∵O、E分别为AD、AB的中点,
∴OA=AE=BE=1,
又∵∠A=∠EBN=90°,∠AEO=∠NEB,
∴△OAE≌△NBE,得OA=BN=1,
同理可得CQ=1;
故NQ=NB+BC+CQ=1+2+1=4,即点K运动了4个单位长度.
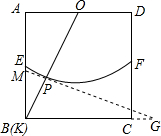 (2)①当K、B重合时,
(2)①当K、B重合时,
∵MG与弧EF所在的圆相切,且切点为P,
∴OB⊥MG,
∴∠BMP+∠OBA=∠BMP+∠BGM=90°,
∴∠OBA=∠BGM,
又∵∠MBG=∠OAB=90°,
∴△OAB∽△MBG,得:
=
,由于BA=2OA,则BG:BM=2.
②存在BG:BM=3的情况,理由如下:
假设存在符合条件的P点,使得BG:BM=3,过K作KH⊥OA于H,
则四边形ABKH为矩形,有KH=AB=2;
∵MG与弧EF相切于点P,
∴OK⊥MG,且垂足为P,
∴∠1+∠2=90°;
又∵∠G+∠2=90°,则∠1=∠G;
∵∠OHK=∠GBM=90°,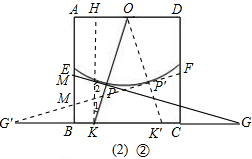
∴△OHK∽△MBG,
∴
=
=
,
∴OH=
,AH=BK=
;
∴存在符合题意的K点,使得BG:BM=3;
同理可得:在线段BC、CD以及CB的延长线上,存在这样的点K′、M″、G′,
使得CK′=
,CG′:CM″=3;
连接G′M″交AB于M′,则BG′:BM′=CG′:CM″=3;
此时BK′=BC-K′C=2-
=
,即BK的值为
或
.
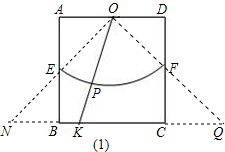
当P从点E运动到点F时,点K从点N运动到了点Q;
∵O、E分别为AD、AB的中点,
∴OA=AE=BE=1,
又∵∠A=∠EBN=90°,∠AEO=∠NEB,
∴△OAE≌△NBE,得OA=BN=1,
同理可得CQ=1;
故NQ=NB+BC+CQ=1+2+1=4,即点K运动了4个单位长度.
 (2)①当K、B重合时,
(2)①当K、B重合时,∵MG与弧EF所在的圆相切,且切点为P,
∴OB⊥MG,
∴∠BMP+∠OBA=∠BMP+∠BGM=90°,
∴∠OBA=∠BGM,
又∵∠MBG=∠OAB=90°,
∴△OAB∽△MBG,得:
| BG |
| BM |
| BA |
| OA |
②存在BG:BM=3的情况,理由如下:
假设存在符合条件的P点,使得BG:BM=3,过K作KH⊥OA于H,
则四边形ABKH为矩形,有KH=AB=2;
∵MG与弧EF相切于点P,
∴OK⊥MG,且垂足为P,
∴∠1+∠2=90°;
又∵∠G+∠2=90°,则∠1=∠G;
∵∠OHK=∠GBM=90°,

∴△OHK∽△MBG,
∴
| OH |
| HK |
| BM |
| BG |
| 1 |
| 3 |
∴OH=
| 2 |
| 3 |
| 1 |
| 3 |
∴存在符合题意的K点,使得BG:BM=3;
同理可得:在线段BC、CD以及CB的延长线上,存在这样的点K′、M″、G′,
使得CK′=
| 1 |
| 3 |
连接G′M″交AB于M′,则BG′:BM′=CG′:CM″=3;
此时BK′=BC-K′C=2-
| 1 |
| 3 |
| 5 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |


练习册系列答案
相关题目

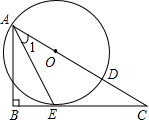

 直线AE与l相交于点D.
直线AE与l相交于点D.



