题目内容
如图,AB为相交两圆⊙O1与⊙O的公切线,且O1在⊙O上,大圆⊙O的半径为4,则公切线AB的长的取值范围为______.
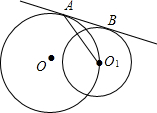

如图,设圆O1的半径为R,连接OA,O1B,OO1,作O1F⊥OA,
由四边形ABO1F是矩形,得AB=FO1;由勾股定理得,OO12=OF2+O1F2,
即42=O1F2+(4-R)2,
整理得,AB=O1F=
=
,
由于两圆相交,则R的取值范围为:0<R<8,
∴0<AB≤4,且当R=4时,AB=4,
故答案为:0<AB≤4.
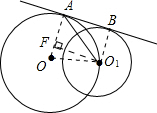
由四边形ABO1F是矩形,得AB=FO1;由勾股定理得,OO12=OF2+O1F2,
即42=O1F2+(4-R)2,
整理得,AB=O1F=
| -R2+8R |
| -(R-4)2+16 |
由于两圆相交,则R的取值范围为:0<R<8,
∴0<AB≤4,且当R=4时,AB=4,
故答案为:0<AB≤4.


练习册系列答案
相关题目