题目内容
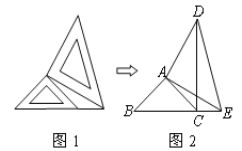
【题目】两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,图中AB=AC,AD=AE,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连结DC.
(1)图2中的全等三角形是_______________,并给予证明(说明:结论中不得含有未标识的字母);
(2)指出线段DC和线段BE的关系,并说明理由.
【答案】(1)△ACD≌△ABE,证明见解析;(2)线段DC和线段BE的关系是:垂直且相等,理由见解析.
【解析】
(1)根据SAS证明△ACD≌△ABE 即可;
(2)线段DC和线段BE的关系是:垂直且相等.利用全等三角形的性质即可证明.
解:(1)图2中的全等三角形是:△ACD≌△ABE.
证明:∵∠BAC=∠EAD=90°,
∴∠BAC+∠CAE=∠EAD+∠CAE,
∴∠BAE=∠CAD,
在△ABE与△ACD中,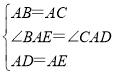 ,
,
∴△ACD≌△ABE(SAS).
故答案为:△ACD≌△ABE;
(2)线段DC和线段BE的关系是:垂直且相等.
理由:由(1)知:△ACD≌△ABE
∴DC=BE,∠ACD=∠B,
∵∠BAC=90°,
∴∠B+∠ACB=90°,
∴∠ACD+∠ACB=90°,即∠BCD=90°,
∴BE⊥DC,
∴线段DC和线段BE的关系是:垂直且相等.

【题目】为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30
【题目】某班对道德与法治,历史,地理三门程的选考情况进行调研,数据如下:
科目 | 道德与法治 | 历史 | 地理 |
选考人数(人) | 19 | 13 | 18 |
其中道德与法治,历史两门课程都选了的有3人,历史,地理两门课程都选了的有4人,该班至多有多少学生( )
A.41B.42C.43D.44

