题目内容
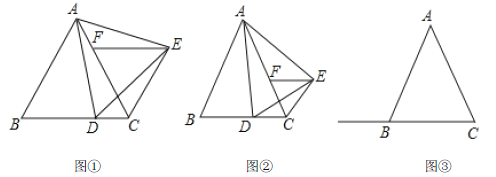
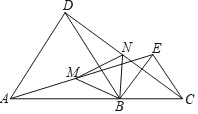
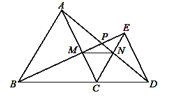
【题目】如图,△ABC和△CDE都是等边三角形,B,C,D三点在一条直线上,AD与BE交于点P,AC,BE交于点M,AD,CE交于点N,连接MN,则下列五个结论:①AD=BE;②∠BMC=∠ANE;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中一定正确的是__________.(填出所有正确结论的序号)
【答案】①③④⑤
【解析】
根据先证明△BCE≌△ACD,得出AD=BE,根据已知给出的条件即可得出答案.
∵△ABC和△DEC都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠ECD=60°,∴∠ACB+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,∴△BCE≌△ACD(SAS),∴AD=BE,故①正确;
∵△BCE≌△ACD,∴∠CBE=∠CAD.
∵∠ACB=∠ACE=60°,∴∠BMC=∠ANC,故②错误;
∵△BCE≌△ACD,∴∠CBE=∠CAD.
∵∠BMC=∠AMP,∴∠APM=∠ACB=60°,故③正确;
在△ACN和△BCM中,∵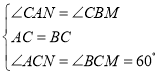 ,∴△ACN≌△BCM,∴AN=BM,故④正确;
,∴△ACN≌△BCM,∴AN=BM,故④正确;
△ACN≌△BCM,∴CM=CN,∴△CMN为等腰三角形.
∵∠MCN=60°,∴△CMN是等边三角形,故⑤正确.
故答案为:①③④⑤.

 名校课堂系列答案
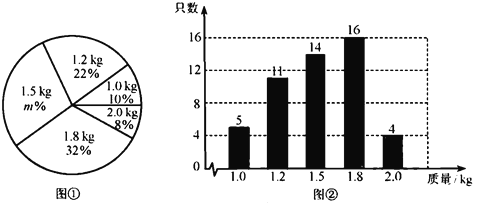
名校课堂系列答案【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 278 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计当![]() 很大时,摸到白球的频率将会接近 (精确到0.1);
很大时,摸到白球的频率将会接近 (精确到0.1);
(2)假如摸一次,摸到黑球的概率![]() ;
;
(3)试估算盒子里黑颜色的球有多少只.
【题目】某天,一蔬菜经营户用 1200 元钱按批发价从蔬菜批发市场买了西红柿和豆角共 400 kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 2.4 | 3.2 |
零售价(单位:元/kg) | 3.8 | 5.2 |
(1)该经营户所批发的西红柿和豆角的质量分别为多少 kg?
(2)如果西红柿和豆角全部以零售价售出,他当天卖出这些西红柿和豆角赚了多少钱?