题目内容
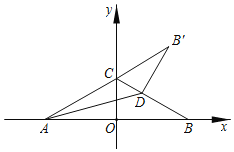
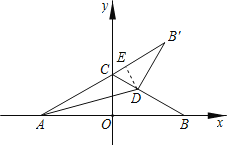
【题目】如图,直线y=![]() x+1分别交x轴、y轴于点A、C,点B是点A关于y的对称点,点D是线段BC上一点,把△ABD沿AD翻折使AB落在射线AC上,得△AB'D,则△ABC与△AB'D重叠部分的面积为( )
x+1分别交x轴、y轴于点A、C,点B是点A关于y的对称点,点D是线段BC上一点,把△ABD沿AD翻折使AB落在射线AC上,得△AB'D,则△ABC与△AB'D重叠部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
首先过点D作DE⊥AB′于点E,由直线的解析式和轴对称的性质求得∠CAB=∠B=30°,AB=2![]() ,利用勾股定理即可求得AC的长,又由折叠的性质,易得∠CDB′=90°,∠B′=30°,B′C=AB′﹣AC=2
,利用勾股定理即可求得AC的长,又由折叠的性质,易得∠CDB′=90°,∠B′=30°,B′C=AB′﹣AC=2![]() ﹣2,继而求得CD与B′D的长,然后求得高DE的长,继而求得答案.
﹣2,继而求得CD与B′D的长,然后求得高DE的长,继而求得答案.
解:过点D作DE⊥AB′于点E,
∵直线y=![]() x+1分别交x轴、y轴于点A、C,
x+1分别交x轴、y轴于点A、C,
∴OA=![]() ,OC=1,∠OAC=30°,
,OC=1,∠OAC=30°,
∴AC=![]() =2,
=2,
∵点B是点A关于y的对称点,
∴OA=OB=![]() ,AC=BC=2,
,AC=BC=2,
∴AB=2![]() ,∠OBC=∠OAC=30°,
,∠OBC=∠OAC=30°,
由折叠的性质得:AB′=AB=2![]() ,∠B′=∠ABC=30°,
,∠B′=∠ABC=30°,
∵∠B′CD=∠CAB+∠ABC=60°,
∴∠CDB′=90°,
∵B′C=AB′﹣AC=2![]() ﹣2,
﹣2,
∴CD=![]() B′C=
B′C=![]() ﹣1,B′D=B′Ccos∠B′=(2
﹣1,B′D=B′Ccos∠B′=(2![]() ﹣2)×
﹣2)×![]() =3﹣
=3﹣![]() ,
,
∴DE=![]() =
=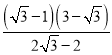 =
=![]() ,
,
∴S重叠=![]() ACDE=
ACDE=![]() ×2×
×2×![]() =
=![]() .
.
故选:A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目