题目内容
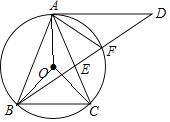
【题目】如图,△ABC内接于⊙O,AB=AC,∠ABC=72°,过点A作BC的平行线与∠ABC的平分线交于点D,BD交AC于点E,交⊙O于点F,连接AF.
(1)求证:AD是⊙O的切线;
(2)已知BC=2,求EF的长.

【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接AO,OB,求出∠OAD=90°即可;
(2)证得△AEF≌△BCE,得出EF=CE,设EF=EC=x,则AC=2+x,证得△ABC∽△BEC,根据相似三角形的性质得出关于x的方程,解方程即可.
(1)证明:连接AO、BO、CO,
∵AB=AC,∠ABC=72°,
∴∠ABC=∠ACB=72°,
∴∠BAC=36°,
在△ABO和△ACO中
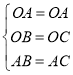 ,
,
∴△ABO≌△ACO(SSS),
∴∠OAC=![]() ∠BAC=18°,
∠BAC=18°,
∵AD∥BC,
∴∠DAC=∠ACB=72°,
∴∠OAD=∠OAC+∠DAC=18°+72°=90°,
∴AD是⊙O的切线;
(2)解:∵∠BAC=∠ABD=36°,
∴AE=BE,
∵∠DBC=36°∠ACB=72°,
∴∠BEC=72°,
∴BE=BC=2,
∴AE=BC,
在△BCE和△AFE中
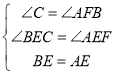 ,
,
∴△AEF≌△BCE(AAS),
∴EF=CE,
设EF=EC=x,则AC=2+x,
∵∠ABC=∠BEC=72°,∠ACB=∠BCE,
∴△ABC∽△BEC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得x=![]() ﹣1或﹣1﹣
﹣1或﹣1﹣![]() (舍去),
(舍去),
∴EF=![]() ﹣1.
﹣1.
故答案为:(1)详见解析;(2)![]() .
.

【题目】同学们设计了一个重复抛掷的实验:全班48人分为8个小组,每组抛掷同一型号的一枚瓶盖300次,并记录盖面朝上的次数,下表是依次累计各小组的实验结果.
1组 | 1~2组 | 1~3组 | 1~4组 | 1~5组 | 1~6组 | 1~7组 | 1~8组 | |
盖面朝上次数 | 165 | 335 | 483 | 632 | 801 | 949 | 1122 | 1276 |
盖面朝上频率 | 0.550 | 0.558 | 0.537 | 0.527 | 0.534 | 0.527 | 0.534 | 0.532 |
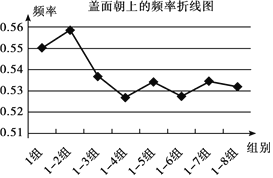
根据实验,你认为这一型号的瓶盖盖面朝上的概率为____,理由是:____.