Question

【题目】如图，在平面直角坐标系中，四边形OABC为矩形，直线y=kx+b交BC于点E（1，m），交AB于点F（4，），反比例函数y=（x＞0）的图象经过点E，F．

（1）求反比例函数及一次函数解析式；

（2）点P是线段EF上一点，连接PO、PA，若△POA的面积等于△EBF的面积，求点P的坐标．

Answer 1

【答案】（1）；；（2）点P坐标为（，）．

【解析】

（1）将F（4，）代入，即可求出反比例函数的解析式；再根据求出E点坐标，将E、F两点坐标代入，即可求出一次函数解析式；

（2）先求出△EBF的面积，

点P是线段EF上一点，可设点P坐标为，

根据面积公式即可求出P点坐标.

解：（1）∵反比例函数经过点，

∴n=2，

反比例函数解析式为．

∵的图象经过点E（1，m），

∴m=2，点E坐标为（1，2）．

∵直线 过点，点，

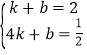∴，解得，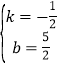

∴一次函数解析式为；

（2）∵点E坐标为（1，2），点F坐标为，

∴点B坐标为（4，2），

∴BE=3，BF=，

∴，

∴ ．

点P是线段EF上一点，可设点P坐标为，

∴，

解得，

∴点P坐标为．