题目内容
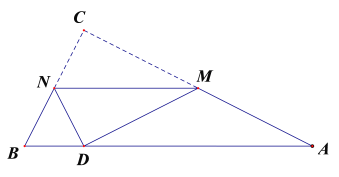
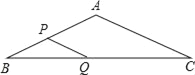
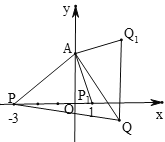
【题目】如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,将线段AP绕点A逆时针旋转90°,得到线段AQ,当点P从点(3,0)运动到点(1,0)时,点Q运动的路径长为____.
【答案】4
【解析】
设点P运动到原点时点Q的对应点是B,连接BQ,根据旋转的性质及同角的余角相等可得∠PAO=∠BAQ,利用SAS可证明△APO≌△AQB,可得∠ABQ=∠AOP=90°,可知点P运动过程中,∠ABQ是定值,即可确定点Q的运动轨迹是经过点B且与AB垂直的线段,设点P运动到点(1,0)时的对应点为P1,点Q的对应点为Q1,连接QQ1,利用SAS可证明△APP1≌△AQQ1,可得PP1=QQ1,根据P、P1的坐标求出PP1的长即可得答案.
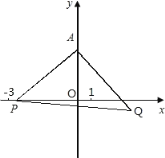
如图,设点P运动到原点时点Q的对应点是B,
∵线AP绕点A逆时针旋转90°,得到AQ,AO绕点A逆时针旋转90°,得到AB,
∴∠PAQ=∠OAB=90°,AP=AQ,AO=AB,
∴∠PAO+∠OAQ=∠QAB+∠OAQ=90°,
∴∠PAO=∠QAB,
在△PAO和△QAB中,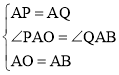 ,
,
∴△PAO≌△QAB,
∴∠ABQ=∠AOP=90°,
∴点P运动过程中,∠ABQ=90°,是定值,
∴点Q的运动轨迹是经过点B且垂直于AB的线段,
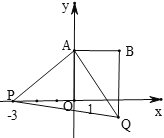
如图,设点P运动到点(1,0)时的对应点为P1,点Q的对应点为Q1,连接QQ1,1
∴QQ1即是点Q运动的距离,
由旋转的性质得AP=AQ,AP1=AQ1,∠PAQ=∠P1AQ1=90°,
∴∠PAP1+∠P1AQ=∠P1AQ+∠QAQ1=90°,
∴∠PAP1=∠QAQ1,
在△APP1和△QAQ1中,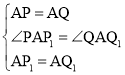 ,
,
∴△APP1≌△QAQ1,
∴PP1=QQ1,
∵点P从点(-3,0)运动到(1,0),
∴QQ1=PP1=1-(-3)=4
故答案为:4

 阅读快车系列答案
阅读快车系列答案