题目内容
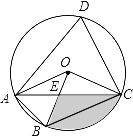
【题目】如图1，在矩形ABCD中，对角线AC与BD相交于点O，过点O作直线EF⊥BD，且交AC于点E，交BC于点F，连接BE、DF，且BE平分∠ABD.
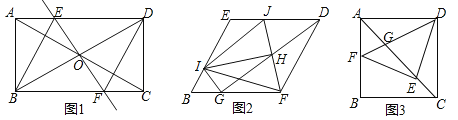
（1）①求证：四边形BFDE是菱形；②求∠EBF的度数．
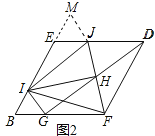
（2）把（1）中菱形BFDE进行分离研究，如图2，G，I分别在BF，BE边上，且BG=BI，连接GD，H为GD的中点，连接FH，并延长FH交ED于点J，连接IJ，IH，IF，IG．试探究线段IH与FH之间满足的数量关系，并说明理由；
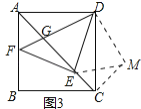
（3）把（1）中矩形ABCD进行特殊化探究，如图3，矩形ABCD满足AB=AD时，点E是对角线AC上一点，连接DE，作EF⊥DE，垂足为点E，交AB于点F，连接DF，交AC于点G．请直接写出线段AG，GE，EC三者之间满足的数量关系．
【答案】（1）①证明见解析；②
；（2）
；（3）
.
【解析】
（1）①由
，推出
，
，推出四边形
是平行四边形，再证明
即可．
②先证明
，推出
，延长即可解决问题．
（2）．只要证明
是等边三角形即可．
（3）结论：．如图3中，将
绕点
逆时针旋转
得到
，先证明
，再证明
是直角三角形即可解决问题．
（1）①证明：如图1中，
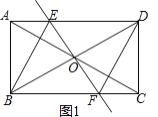
四边形
是矩形，
，
，
，
在
和
中，
，
，
，，
四边形是平行四边形，
，，
，
四边形是菱形．
②
平分
，
，
，
，
，
，
，
，
，
．
（2）结论：．
理由：如图2中，延长
到
，使得
，连接
．
四边形是菱形，
，
，
，
，
在
和
中，
，
，
，
，
，
，
，
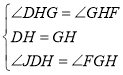是等边三角形，
，
在
和
中，
，
，
，
，
，
，
，
，
，
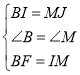是等边三角形，
在
中，
，
，
，
．
（3）结论：．
理由：如图3中，将绕点逆时针旋转得到，
，
四点共圆，
，
，
，
，
，
在
和
中，
，
，
，
，
，
，
，，
．
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
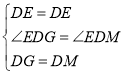【题目】一家公司准备招聘一名英文翻译，对甲、乙和丙三名应试者进行了听、说、读、写 的英语水平测试，他们各项的成绩（百分制）如下：
应试者 | 听 | 说 | 读 | 写 |
甲 | 82 | 86 | 78 | 75 |
乙 | 73 | 80 | 85 | 82 |
丙 | 81 | 82 | 80 | 79 |
（1）如果这家公司按照这三名应试者的平均成绩（百分制）计算，从他们的成绩看，应该录取谁？
（2）如果这家公司想招一名口语能力较强的翻译，听、说、读、写成绩按照 3∶4∶2∶1 的权重确定，计算三名应试者的平均成绩（百分制），从他们的成绩看， 应该录取谁？
（3）如果这家公司想招一名笔译能力较强的翻译，听、说、读、写成绩按照 1∶2∶3∶4 的权重确定，计算三名应试者的平均成绩（百分制）．从他们的成绩看， 应该录取谁？
【题目】某超市拟购进甲乙两种大米，购进计划见下表：
品种 项目 | 数量 （单位：kg） | 进价 （单位：元/kg） | 售价的设定标准 |
甲种大米 | 600 | a | 在进价的基础上提高40％ |
乙种大米 | 800 | b | 在进价的基础上提高30％ |
（1）若计划购进的大米全部售出，超市可获利多少元？(用含有a,b的代数式表示结果）
（2）由于包装袋破损，两种大米混合在一起，无法分装，超市决定以散装米出售，售价为
元/kg，若这批大米全部售出，超市是赚钱还是亏本，请说明理由？
