ЬтФПФкШн
ЁОЬтФПЁПбЇаЃзМБИдкИїАрЩшСЂЭМЪщНЧвдЗсИЛЭЌбЇУЧЕФПЮгрЮФЛЏЩњЛюЃЎЮЊСЫИќКЯРэЕФДюХфИїРрЪщМЎЃЌбЇаЃЭХЮЏвдЁАЮвзюЯВАЎЕФЪщМЎЁБЮЊжїЬтЃЌЖдбЇЩњзюЯВАЎЕФвЛжжЪщМЎРраЭНјааЫцЛњГщбљЕїВщЃЌЪеМЏећРэЪ§ОнКѓЃЌЛцжЦГівдЯТСНЗљЮДЭъГЩЕФЭГМЦЭМЃЌЧыИљОнЭМЂйКЭЭМЂкЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
 ЁЁЁЁЁЁЁЁ
ЁЁЁЁЁЁЁЁ
ЃЈ1ЃЉдкетДЮГщбљЕїВщжаЃЌвЛЙВЕїВщСЫ_____________УћбЇЩњЃЛ
ЃЈ2ЃЉЧыАбелЯпЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉдкЭГМЦЭМЂкжаЃЌЧѓГіЁАЬхг§ЁБВПЗжЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЃЛ
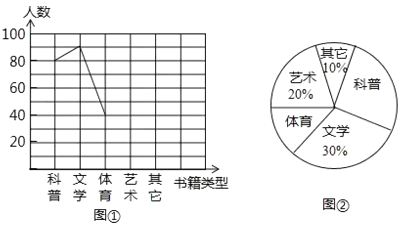
ЃЈ4ЃЉШєИУаЃгабЇЩњ2400ШЫЃЌЙРМЦЯВЛЖЁАПЦЦеЁБЪщМЎЕФгаЖрЩйШЫЃП
ЁОД№АИЁПЃЈ1ЃЉ300УћЃЛЃЈ2ЃЉД№АИМћНтЮіЃЛЃЈ3ЃЉ48ЁуЃЛЃЈ4ЃЉ640ШЫЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉ гУзюЯВАЎЮФзжРрЕФШЫЪ§Г§вдзюЯВАЎЮФзжРрЕФЫљеМАйЗжБШМДПЩЧѓНтвЛЙВЕїВщЕФбЇЩњЕФзмШЫЪ§МДбљБОзмСПЃЛ
ЃЈ2ЃЉгУзюЯВАЎвеЪѕРрЫљеМЕФАйЗжБШГЫвдВЮгыЕїВщЕФзмШЫЪ§ЧѓНтзюЯВАЎвеЪѕРрЕФзмШЫЪ§ЃЌгУЦфЫќЫљеМЕФАйЗжБШГЫвдЕїВщШЫЪ§ЕФзмШЫЪ§ЧѓНтЦфЫќЕФШЫЪ§ЃЌИљОнЫљЧѓВЙГфелЯпЭГМЦЭММДПЩЃЛ
ЃЈ3ЃЉгУзюЯВАЎЬхг§РрЫљеМЕФАйЗжБШГЫвд360ЁуМДПЩЧѓГіЦфЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ4ЃЉгЩбљБОЙРМЦзмЬхПЩЕУЃЌгУзюЯВАЎПЦЦеЫљеМЕФАйЗжБШГЫвдИУжабЇЕФбЇЩњзмЪ§МДПЩЧѓНт.
ЃЈ1ЃЉЃКгЩЕквЛИіелЯпЭМПЩвджЊЕРзюЯВАЎЮФзжРрЕФШЫЪ§ЮЊ90ШЫЃЌ
ДгЕкЖўИіЩШаЮЭМПЩвджЊЕРзюЯВАЎЮФзжРрЕФЫљеМАйЗжБШЪЧ30ЃЅЃЌ
ЫљвдЕїВщзмШЫЪ§ЃК![]() ЃЈУћЃЉЃЌ
ЃЈУћЃЉЃЌ
вђДЫЃЌдкетДЮГщбљЕїВщжаЃЌвЛЙВЕїВщСЫ300УћбЇЩњЃЛ
ЃЈ2ЃЉЃКгЩЃЈ1ЃЉжЊЕїВщзмШЫЪ§ЪЧ300ЃЌвђДЫПЩЕУ:
ЯВАЎвеЪѕЕФгаЃК![]() (Ућ)ЃЌ
(Ућ)ЃЌ
ЯВАЎЦфЫќЕФгаЃК![]() (Ућ)
(Ућ)
ВЙШЋЕФелЯпЭГМЦЭМЃЌШчЯТЭМЫљЪОЃК

ЃЈ3ЃЉЃКЮвУЧжЊЕРЃЌдВЫљЖдгІЕФдВаФНЧЪЧ![]() ЃЌ
ЃЌ
ДгЭМ1жЊЕРзюЯВАЎЬхг§ЕФШЫЪ§га40УћЃЌЕїВщзмШЫЪ§ЪЧ300УћЃЌ
вђДЫЃЌЁАЬхг§ЁБВПЗжЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЃК![]() ЃЌ
ЃЌ
Д№ЃКдкЭГМЦЭМЂкжаЃЌЁАЬхг§ЁБВПЗжЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЮЊ![]() ЃЎ
ЃЎ
ЃЈ4ЃЉЃКДгЭМ1ЕФелЯпЭМжЊЕРзюЯВАЎПЦЦеЕФШЫЪ§га80УћЃЌЕїВщзмШЫЪ§ЕФЮЊ300УћЃЌ
ЫљвдИУаЃЯВЛЖЁАПЦЦеЁБЪщМЎЕФДѓдМгаЃК![]() (ШЫ)
(ШЫ)
Д№ЃКЙРМЦИУаЃЯВЛЖЁАПЦЦеЁБЪщМЎЕФДѓдМга640ШЫ.

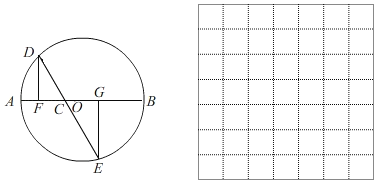
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌAB=4cmЃЌCЮЊABЩЯвЛЖЏЕуЃЌЙ§ЕуCЕФжБЯпНЛЁбOгкDЁЂEСНЕуЃЌЧвЁЯACD=60ЁуЃЌDFЁЭABгкЕуFЃЌEGЁЭABгкЕуGЃЌЕБЕуCдкABЩЯдЫЖЏЪБЃЌЩшAF=xcmЃЌDE=ycm(ЕБxЕФжЕЮЊ0Лђ3ЪБЃЌyЕФжЕЮЊ2)ЃЌЬНОПКЏЪ§yЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩЃЎ
ЃЈ1ЃЉЭЈЙ§ШЁЕуЁЂЛЭМЁЂВтСПЃЌЕУЕНСЫxгыyЕФМИзщЖдгІжЕЃЌШчЯТБэЃК
x/cm | 0 | 0.40 | 0.55 | 1.00 | 1.80 | 2.29 | 2.61 | 3 |
y/cm | 2 | 3.68 | 3.84 | 3.65 | 3.13 | 2.70 | 2 |
ЃЈ2ЃЉНЈСЂЦНУцжБНЧзјБъЯЕЃЌУшГівдВЙШЋКѓЕФБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ3ЃЉНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕуFгыЕуOжиКЯЪБЃЌDEГЄЖШдМЮЊЁЁЁЁЁЁЁЁcm(НсЙћБЃСєвЛЮЛаЁЪ§)ЃЎ