题目内容
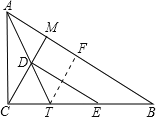
【题目】已知:如图,△ABC中,∠C=90°,CM⊥AB于M,AT平分∠BAC交CM于D,交BC于T,过D作DE∥AB交BC于E,求证CT=BE
.
【答案】见解析
【解析】
过T作TF⊥AB于F,根据角平分线上的点到角的两边的距离相等得TF=CT,再根据角平分线的定义和等角的余角相等的性质得到∠CDT=∠CTD,所以CD=CT,再证明△CDE和△TFB全等,然后根据全等三角形对应边相等可以得到CE=TB,都减去TE即可得到CT=BE.
证明:过T作TF⊥AB于F,
∵AT平分∠BAC,∠ACB=90°,
∴CT=TF(角平分线上的点到角两边的距离相等),
∵∠ACB=90°,CM⊥AB,
∴∠ADM+∠DAM=90°,∠ATC+∠CAT=90°,
∵AT平分∠BAC,
∴∠DAM=∠CAT,
∴∠ADM=∠ATC,
∴∠CDT=∠CTD,
∴CD=CT,
又∵CT=TF(已证),
∴CD=TF,
∵CM⊥AB,DE∥AB,
∴∠CDE=90°,∠B=∠DEC,
在△CDE和△TFB中,
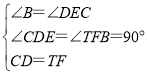 ,
,
∴△CDE≌△TFB(AAS),
∴CE=TB,
∴CE-TE=TB-TE,
即CT=BE.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目