ЬтФПФкШн
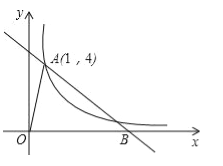
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌКЏЪ§y=2x+8ЕФЭМЯѓЗжБ№НЛxжсЁЂyжсгкAЁЂBСНЕуЃЌЙ§ЕуAЕФжБЯпНЛyжсе§АыжсгкЕуMЃЌЧвЕуMЮЊЯпЖЮOBЕФжаЕуЃЎ

ЃЈ1ЃЉЧѓжБЯпAMЕФКЏЪ§НтЮіЪНЃЎ
ЃЈ2ЃЉЪддкжБЯпAMЩЯеввЛЕуPЃЌЪЙЕУSЁїABP=SЁїAOBЃЌЧѓГіЕуPЕФзјБъЃЎ
ЃЈ3ЃЉШєЕуHЮЊзјБъЦНУцФкШЮвтвЛЕуЃЌдкзјБъЦНУцФкЪЧЗёДцдкетбљЕФЕуHЃЌЪЙвдAЁЂBЁЂMЁЂHЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЫљгаЕуHЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=x+4ЃЛЃЈ2ЃЉЕуPЕФзјБъЮЊЃЈ-12ЃЌ-8ЃЉЛђЃЈ4ЃЌ8ЃЉЃЛЃЈ3ЃЉДцдкЃЌЃЈ-4ЃЌ-4ЃЉЃЌЃЈ-4ЃЌ4ЃЉЛђЃЈ4ЃЌ12ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЭЈЙ§КЏЪ§y=2x+8ЧѓГіAЁЂMСНЕузјБъЃЌгЩСНЕузјБъЧѓГіжБЯпAMЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЩшГіPЕузјБъЃЌАДееЕШСПЙиЯЕЁАSЁїABP=SЁїAOBЁБМДПЩЧѓГіЃЛ
ЃЈ3ЃЉЩшЕуHЕФзјБъЮЊЃЈmЃЌnЃЉЃЌШЛКѓЗжШ§жжЧщПіНјааЬжТлМДПЩ.
ЃЈ1ЃЉЕБx=0ЪБЃЌy=2x+8=8ЃЌ
ЁрЕуBЕФзјБъЮЊЃЈ0ЃЌ8ЃЉЃЛ
ЕБy=0ЪБЃЌ2x+8=0ЃЌ
НтЕУЃКx=-4ЃЌ
ЁрЕуAЕФзјБъЮЊЃЈ-4ЃЌ0ЃЉЃЎ
ЁпЕуMЮЊЯпЖЮOBЕФжаЕуЃЌ
ЁрЕуMЕФзјБъЮЊЃЈ0ЃЌ4ЃЉЃЎ
ЩшжБЯпAMЕФКЏЪ§НтЮіЪНЮЊy=kx+bЃЈkЁй0ЃЉЃЌ
НЋAЃЈ-4ЃЌ0ЃЉЃЌBЃЈ0ЃЌ4ЃЉДњШыy=kx+bЃЌЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпAMЕФКЏЪ§НтЮіЪНЮЊy=x+4ЃЎ
ЃЈ2ЃЉЩшЕуPЕФзјБъЮЊЃЈxЃЌx+4ЃЉЃЌ
ЁпSЁїABP=SЁїAOBЃЌ
Ёр![]() BM|xP-xA|=
BM|xP-xA|=![]() OAOBЃЌМД
OAOBЃЌМД![]() ЁС4ЁС|x+4|=
ЁС4ЁС|x+4|=![]() ЁС4ЁС8ЃЌ
ЁС4ЁС8ЃЌ
НтЕУЃКx1=-12ЃЌx2=4ЃЌ
ЁрЕуPЕФзјБъЮЊЃЈ-12ЃЌ-8ЃЉЛђЃЈ4ЃЌ8ЃЉЃЎ
ЃЈ3ЃЉДцдкЃЌ ЃЈ-4ЃЌ-4ЃЉЃЌЃЈ-4ЃЌ4ЃЉЛђЃЈ4ЃЌ12ЃЉЃЎ
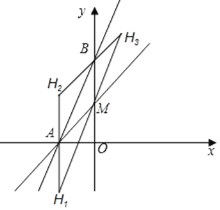
ЩшЕуHЕФзјБъЮЊЃЈmЃЌnЃЉЃЎ
ЗжШ§жжЧщПіПМТЧЃЈШчЭМЫљЪОЃЉЃК
ЂйЕБAMЮЊЖдНЧЯпЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрЕуH1ЕФзјБъЮЊЃЈ-4ЃЌ-4ЃЉЃЛ
ЂкЕБABЮЊЖдНЧЯпЪБЃЌ ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрЕуH2ЕФзјБъЮЊЃЈ-4ЃЌ4ЃЉЃЛ
ЂлЕБBMЮЊЖдНЧЯпЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрЕуH3ЕФзјБъЮЊЃЈ4ЃЌ12ЃЉЃЎ
злЩЯЫљЪіЃКдкзјБъЦНУцФкДцдкЕуHЃЌЪЙвдAЁЂBЁЂMЁЂHЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЕуHЕФзјБъЮЊЃЈ-4ЃЌ-4ЃЉЃЌЃЈ-4ЃЌ4ЃЉЛђЃЈ4ЃЌ12ЃЉЃЎ