题目内容
【题目】如图,在航线l的两侧分别有观测点A和B,点A到航线![]() 的距离为2km,点B位于点A北偏东60°方向且与A相距10km.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5分钟后该轮船行至点A的正北方向的D处.
的距离为2km,点B位于点A北偏东60°方向且与A相距10km.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5分钟后该轮船行至点A的正北方向的D处.
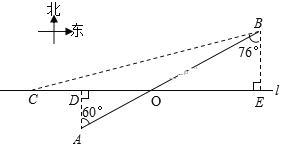
(1)求观测点B到航线![]() 的距离;
的距离;
(2)求该轮船航行的速度(结果精确到0.1km/h).
(参考数据: ![]() ≈1.73,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
≈1.73,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
【答案】(1)观测点![]() 到航线
到航线![]() 的距离为3km(2)该轮船航行的速度约为40.6km/h
的距离为3km(2)该轮船航行的速度约为40.6km/h
【解析】试题分析:(1)设AB与l交于点O,利用∠DAO=60°,利用∠DAO的余弦求出OA长,从而求得OB长,继而求得BE长即可;
(2)先计算出DE=EF+DF=求出DE=5![]() ,再由进而由tan∠CBE=
,再由进而由tan∠CBE=![]() 求出EC,即可求出CD的长,进而求出航行速度.
求出EC,即可求出CD的长,进而求出航行速度.
试题解析:(1)设AB与l交于点O,
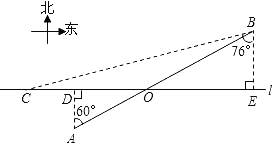
在Rt△AOD中,
∵∠OAD=60°,AD=2(km),
∴OA=![]() =4(km),
=4(km),
∵AB=10(km),
∴OB=AB﹣OA=6(km),
在Rt△BOE中,∠OBE=∠OAD=60°,
∴BE=OBcos60°=3(km),
答:观测点B到航线l的距离为3km;
(2)∵∠OAD=60°,AD=2(km),∴OD=AD·tan60°=2![]() ,
,
∵∠BEO=90°,BO=6,BE=3,∴OE=![]() =3
=3![]() ,
,
∴DE=OD+OE=5![]() (km);
(km);
CE=BEtan∠CBE=3tan76°,
∴CD=CE﹣DE=3tan76°﹣5![]() ≈3.38(km),
≈3.38(km),
∵5(min)=![]() (h),∴v=
(h),∴v= =12CD=12×3.38≈40.6(km/h),
=12CD=12×3.38≈40.6(km/h),
答:该轮船航行的速度约为40.6km/h.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】某校七年级1至4班计划每班购买数量相同的图书布置班级读书角,但是由于种种原因,实际购书量与计划有出入,下表是实际购书情况:
班级 | 1班 | 2班 | 3班 | 4班 |
实际购买量(本) | a | 33 | c | 21 |
实际购买量与计划购数量的差值(本) | +12 | b | -8 | -9 |
(1) 直接写出a=__________,b=__________,c=__________
(2) 根据记录的数据可知4个班实际购书共_________本
(3) 书店给出一种优惠方案:一次购买不少于15本,其中2本书免费.若每本书售价为30元,请计算这4个班整体购书的最低总花费是多少元?
【题目】已知![]() 是由
是由![]() 经过平移得到的,其中A,B,C三点的对应点分别是
经过平移得到的,其中A,B,C三点的对应点分别是![]() ,
,![]() ,
,![]() ,它们在平面直角坐标系中的坐标如下表所示:
,它们在平面直角坐标系中的坐标如下表所示:
|
|
|
|
|
|
|
|
(1)观察表中各对应点坐标的变化,并填空:![]() __________,
__________,![]() __________.
__________.
(2)在下图的平面直角坐标系中画出![]() 和
和![]() .
.
(3)写出![]() 是怎样平移得到
是怎样平移得到![]() 的?
的?