Question

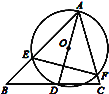
【题目】如图，AB是半圆O的直径，D是半圆O上一点，连接OD，BD，∠ABD＝30°，过A点作半圆O的切线交OD的延长线于点G，点E是上的一个动点，连接AD、DE、BE.

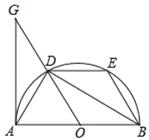
（1）求证：△ADG≌△BOD；

（2）填空：

①当∠DBE的度数为　 时，四边形DOBE是菱形；

②连接OE，当∠DBE的度数为　 时，OE⊥BD．

Answer 1

【答案】（1）见解析；（2）①30°；②30°．

【解析】

（1）先根据圆周角定理易证△AOD是等边三角形，再根据切线的性质得到∠GAO＝90°，然后通过“角边角”即可得证；

（2）①因为BD是菱形DOBE的对角线，根据菱形的对角线平分对角即可得解；

②由（1）知，∠BOD＝120°，由OE⊥BD，可得∠DOE＝∠BOE＝60°，再根据圆周角定理即可得解.

（1）∵OB＝OD，

∴∠ODB＝∠OBD＝30°，

∴∠AOD＝2∠ABD＝60°，

∵OA＝OD，

∴△AOD是等边三角形，

∴∠ADO＝60°，OA＝OD＝AD，

∴∠ADG＝∠DOB＝120°，

∵AG切⊙O于A，

∴∠GAO＝90°，

∴∠GAD＝30°＝∠OBD，

∴△ADG≌△BOD（ASA）；

（2）∵BD是菱形DOBE的对角线，

∴∠DBE＝∠OBD＝30°，

即：当∠DBE＝30°时，四边形DOBE是菱形，

故答案为30°；

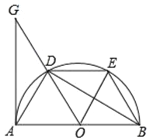
（3）如图，

由（1）知，∠BOD＝120°，

∵OE⊥BD，

∴∠DOE＝∠BOE＝∠BOD＝×120°＝60°，

∴∠DBE＝∠DOE＝×60°＝30°，

故答案为：30°．