题目内容
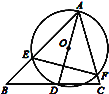
【题目】如图,∠BAC=60°,∠ABC=45°,AB=![]() ,D是线段BC上的一个动点,以AD为直径画圆O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为( )
,D是线段BC上的一个动点,以AD为直径画圆O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由垂线段的性质和圆周角定理以及解直角三角形解答即可.
由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径AD最短,如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
则EH=FH,
∵在Rt△ADB中,∠ABC=45°,AB=4![]() ,
,
∴AD=BD=![]() AB=4,即此时圆的直径为4,
AB=4,即此时圆的直径为4,
∴OE=2,
由圆周角定理可知∠EOH=![]() ∠EOF=∠BAC=60°,
∠EOF=∠BAC=60°,
∴在Rt△EOH中,EH=OEsin∠EOH=2×![]() =
=![]() ,
,
由垂径定理可知EF=2EH=2![]() .
.
故选:B.

练习册系列答案
相关题目
【题目】《朗读者》自播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,沭阳县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示。
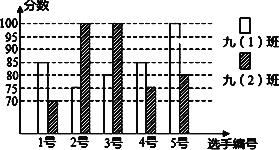
⑴根据图示填写表格;
平均数 | 中位数 | 众数 | |
九⑴班 | 85 | 85 | |
九⑵班 | 80 |
⑵如果规定成绩较稳定的班级胜出,你认为哪个班级能胜出?说明理由。
【题目】某公司有![]() 型产品
型产品![]() 件,
件,![]() 型产品
型产品![]() 件,分配给下属甲、乙两个商店销售,其中
件,分配给下属甲、乙两个商店销售,其中![]() 件给甲店,
件给甲店,![]() 件给乙店,且都能卖完,两商店销售这两种产品每件的利润(元)如下表:
件给乙店,且都能卖完,两商店销售这两种产品每件的利润(元)如下表:
|
| |
甲店 |
|
|
乙店 |
|
|
(1)设分配给甲店![]() 型产品x件,则:
型产品x件,则:
①分配给乙店的![]() 型产品_________件;
型产品_________件;
②分配给乙店的![]() 型产品_________件.
型产品_________件.
(2)这家公司卖出这![]() 件产品的总利润为
件产品的总利润为![]() (元),求
(元),求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(3)若公司要求总利润不低于![]() 元,说明有多少种不同分配方案,并将各种方案设计出来.
元,说明有多少种不同分配方案,并将各种方案设计出来.