题目内容
【题目】已知二次函数y＝﹣x2+2x+m．
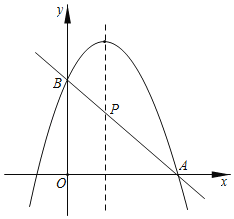
（1）如果二次函数的图象与x轴有两个交点，求m的取值范围；
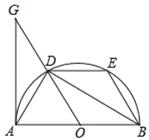
（2）如图，二次函数的图象过点A（3，0），交y轴于B，D是顶点，求△ABD的面积．
（3）在（2）的条件下，根据图象直接写出使一次函数值大于二次函数值的x的取值范围．
【答案】（1）m＞﹣1；（2）6；（3）x＜0或x＞3
【解析】
（1）由题意得：△＝4+4m＞0，即可求解；
（2）故直线AB的表达式为：y＝﹣x+3，设AB交函数对称轴于点P（1，2），△ABD的面积＝
PD×OA，即可求解；
（3）点A、B的横坐标分别为：3，0，即可求解．
解：（1）由题意得：△＝4+4m＞0，解得：m＞﹣1；
（2）将点A坐标代入抛物线表达式得：0＝﹣9+6+m，解得：m＝3，
故抛物线的表达式为：y＝﹣x2+2x+3，令y＝0，则x＝﹣1或3，令x＝0，则y＝3，
故点B（0，3），抛物线于x轴另外一个交点的坐标为C：（﹣1，0），
函数的对称轴为：x＝1，顶点D的坐标为：（1，4），
将点A、B的坐标代入一次函数表达式：y＝kx+b得：
，解得：
，
故直线AB的表达式为：y＝﹣x+3，设AB交函数对称轴于点P（1，2），
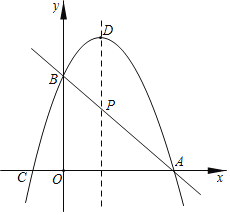
则PD＝4﹣2＝2，
则：△ABD的面积＝
PD×OA＝4×3＝6；
（3）点A、B的横坐标分别为：3，0，
故一次函数值大于二次函数值的x的取值范围：x＜0或x＞3．
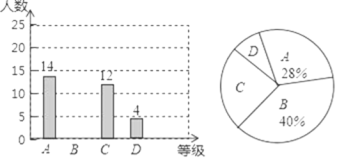
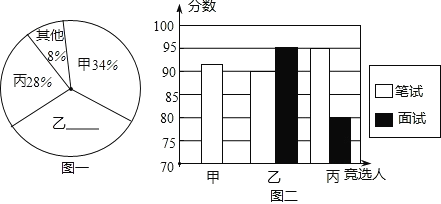
【题目】某初中学校欲向高一级学校推荐一名学生，根据规定的推荐程序：首先由本年级200名学生民主投票，每人只能推荐一人(不设弃权票)，选出了票数最多的甲、乙、丙三人.投票结果统计如图一：
其次，对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示：
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题：
(1)补全图一和图二；
(2)请计算每名候选人的得票数；
(3)若每名候选人得一票记1分，投票、笔试、面试三项得分按照2:5:3的比确定，计算三名候选人的平均成绩，成绩高的将被录取，应该录取谁?
