题目内容
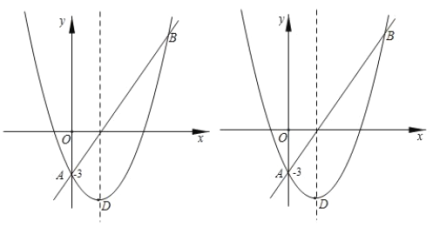
【题目】已知,如图1,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为C与x轴交于A、B两点(点A在点B左侧),点C、B关于过点A的直线l:y=kx+![]() 对称.
对称.
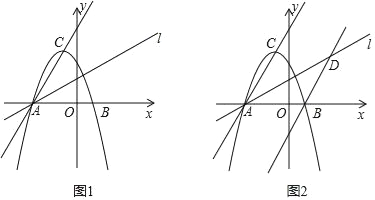
(1)求A、B两点坐标及直线l的解析式;
(2)求二次函数解析式;
(3)如图2,过点B作直线BD∥AC交直线l于D点,M、N分别为直线AC和直线l上的两个动点,连接CN,MM、MD,求CN+NM+MD的最小值.
【答案】(1) 点A、B的坐标分别为(﹣3,0)、(1,0),直线l的表达式为:y=![]() x+
x+![]() ;(2) 二次函数解析式为:y=﹣
;(2) 二次函数解析式为:y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ;(3)8.
;(3)8.
【解析】
(1)y=ax2+2ax﹣3a,令y=0,则x=﹣1或3,即可求解;
(2)设点C的坐标为(﹣1,m),点C、B关于过点A的直线l:y=kx+![]() 对称得AC2=AB2,即可求解;
对称得AC2=AB2,即可求解;
(3)连接BC,则CN+MN的最小值为MB(即:M、N、B三点共线),作D点关于直线AC的对称点Q交y轴于点E,则MB+MD的最小值为BQ(即:B、M、Q三点共线),则CN+MN+MD的最小值=MB+MD的最小值=BQ,即可求解.
解:(1)y=ax2+2ax﹣3a,令y=0,则x=﹣1或3,
即点A、B的坐标分别为(﹣3,0)、(1,0),
点A坐标代入y=kx+![]() 得:0=﹣3k+
得:0=﹣3k+![]() ,解得:
,解得:![]()
即直线l的表达式为:![]() ①,
①,
同理可得直线AC的表达式为: ![]()
直线BD的表达式为:![]() ②,
②,
联立①②并解得:x=3,在点D的坐标为(3,2![]() );
);
(2)设点C的坐标为(﹣1,m),点C、B关于过点A的直线l:y=kx+![]() 对称得AC2=AB2,
对称得AC2=AB2,
即:(﹣3+1)2+m2=16,解得:![]() (舍去负值),点C(1,2
(舍去负值),点C(1,2
将点C的坐标代入二次函数并解得:![]()
故二次函数解析式为: ![]()
(3)连接BC,则CN+MN的最小值为MB(即:M、N、B三点共线),
作D点关于直线AC的对称点Q交y轴于点E,则MB+MD的最小值为BQ(即:B、M、Q三点共线),
则CN+MN+MD的最小值=MB+MD的最小值=BQ,
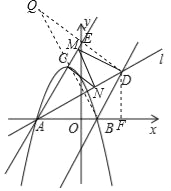
∵DQ⊥AC,AC∥BD,∴∠QDB=90°,
作DF⊥x轴交于点F,
DF=ADsin∠DAF![]()
∵B、C关于直线l对称,即直线l是∠EAF的平分线,
∴ED=FD=2![]() ,
,
则QD=4![]() ,BD=4,
,BD=4,
∴BQ![]()
即CN+NM+MD的最小值为8.

 名校课堂系列答案
名校课堂系列答案【题目】《朗读者》自播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,沭阳县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示。
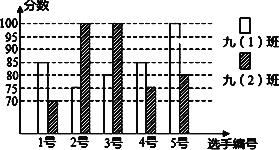
⑴根据图示填写表格;
平均数 | 中位数 | 众数 | |
九⑴班 | 85 | 85 | |
九⑵班 | 80 |
⑵如果规定成绩较稳定的班级胜出,你认为哪个班级能胜出?说明理由。
【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:
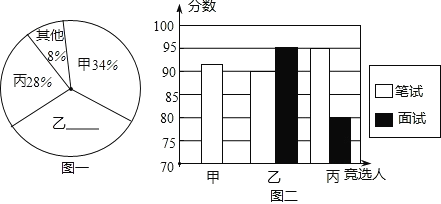
其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?