题目内容
1.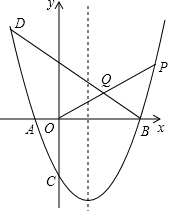 如图,已知抛物线y=ax2+bx+c过点D(-2,5),与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-3).
如图,已知抛物线y=ax2+bx+c过点D(-2,5),与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-3).(1)求此函数的解析式;
(2)若点M在抛物线的对称轴上,点N在抛物线上,是否存在以点M、N、O、B为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,说明理由;
(3)点P是第一象限抛物线上的点,连接OP、BP、OP与BD交于点Q,若△OBP的面积是△OBQ面积的2倍,求点P的坐标.
分析 (1)用待定系数法直接求出抛物线解析式;
(2)先确定出OB=3,分AB为边和为对角线两种情况讨论计算,当AB为边时,有MN∥OB,MN=OB=3建立方程求解即可,当AB为对角线时,MN必过AB的中点建立方程求解即可;
(3)利用三角形的面积关系得出点Q是OP的中点,建立方程组求解即可.
解答 解:(1)∵抛物线y=ax2+bx+c过点D(-2,5),与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-3).
∴$\left\{\begin{array}{l}{4a-2b+c=5}\\{a-b+c=0}\\{c=-3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$,
∴此函数的解析式为y=x2-2x-3,
(2)由(1)知,函数的解析式为y=x2-2x-3,
∴B(3,0),
∴OB=3,抛物线的对称轴为x=1,
∵以点M、N、O、B为顶点的四边形是平行四边形,
∴①当AB为平行四边形的边时,
∴MN∥OB,MN=OB=3,
设点N(m,m2-2m-3),
∴M(1,m2-2m-3),
∴MN=|m-1|=3,
∴m=-2或m=4,
∴N(-2,5)或(4,5),
②当AB为对角线时,MN必过OB的中点G($\frac{3}{2}$,0),
设点N(m,m2-2m-3),M(1,n),
∴$\frac{m+1}{2}=\frac{3}{2}$,$\frac{{m}^{2}-2m-3+n}{2}=0$,
∴m=2,n=3,
∴N(2,-3),
即:满足条件的点N的坐标为(-2,5)或(4,5)或(2,-3).
(3)∵D(-2,5),b(3,0),
∴直线BD解析式为y=-x+3,
∵△OBP的面积是△OBQ面积的2倍,
∴S△OBQ=S△PBQ,
∴BQ是△OBP的边OP的中线,
∴OQ=PQ,
设P(p,p2-2p-3)(p>0),
∵O(0,0),
∴Q($\frac{p}{2}$,$\frac{{p}^{2}-2p-3}{2}$),
∵Q点直线BD上,
∴-$\frac{p}{2}$+3=$\frac{{p}^{2}-2p-3}{2}$,
∴p=$\frac{1-\sqrt{37}}{2}$(舍)或p=$\frac{1+\sqrt{37}}{2}$,
∴P($\frac{1+\sqrt{37}}{2}$,$\frac{11-\sqrt{37}}{2}$).
点评 此题是二次函数综合题,主要考查了待定系数法,平行四边形的性质,三角形的中线,用分类讨论的思想是解本题的关键,用中点坐标公式是解本题的难点,是一道中等难度的中考常考题.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案| A. | y=2(x-1)2+5 | B. | y=2(x-1)2+1 | C. | y=2(x+1)2+3 | D. | y=2(x-3)2+3 |
 实数a,b在数轴上的位置如图所示,以下说法正确的是( )
实数a,b在数轴上的位置如图所示,以下说法正确的是( )| A. | a+b>0 | B. | |a-b|=a-b | C. | |b|>|a| | D. | (a+1)(b-1)>0 |
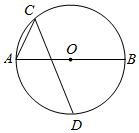 如图.AB是⊙O的直径,∠BAC=60°,D为半圆的中点,若⊙O的半径为4,求CD的长.
如图.AB是⊙O的直径,∠BAC=60°,D为半圆的中点,若⊙O的半径为4,求CD的长.