题目内容
如图，AC是圆O的直径，PA切圆O于点A，弦BC∥OP，OP交圆O于点D，连接PB
（1）求证：PB是圆O的切线；
（2）若PA=3，PD=2，求圆O的半径R的长．
（1）求证：PB是圆O的切线；
（2）若PA=3，PD=2，求圆O的半径R的长．
（1）证明：连接OB，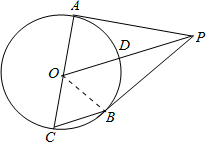
∵OP∥BC
∴∠AOP=∠C，∠BOP=∠OBC，
∵OB=OC，
∴∠C=∠OBC，
∴∠AOP=∠BOP，
∵OA=OB，OP=OP，
∴△AOP≌△BOP，
∴∠OBP=∠OAP，
∵PA切圆O于点A，
∴∠A=90°，
∴∠OBP=90°，
即OB⊥PB，
∴PB是圆O的切线，
（2）∵PA是圆的切线，
∴OA⊥AP，
∴△AOP是直角三角形，
在Rt△AOP中，由勾股定理得，（R+2）2=R2+32
解得R=
．
∵OP∥BC
∴∠AOP=∠C，∠BOP=∠OBC，
∵OB=OC，
∴∠C=∠OBC，
∴∠AOP=∠BOP，
∵OA=OB，OP=OP，
∴△AOP≌△BOP，
∴∠OBP=∠OAP，
∵PA切圆O于点A，
∴∠A=90°，
∴∠OBP=90°，
即OB⊥PB，
∴PB是圆O的切线，
（2）∵PA是圆的切线，
∴OA⊥AP，
∴△AOP是直角三角形，
在Rt△AOP中，由勾股定理得，（R+2）2=R2+32
解得R=
| 5 |
| 4 |
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
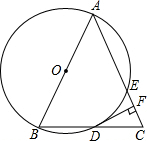
点F，P为ED的延长线上一点．
45°．