题目内容
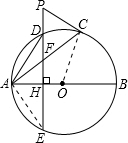
如图，AB、AC分别是⊙O的直径和弦，D为劣弧
上一点，DE⊥AB于点H，交⊙O于点E，交AC于
点F，P为ED的延长线上一点．
（1）当△PCF满足什么条件时，PC与⊙O相切．为什么？
（2）当点D在劣弧
的什么位置时，才能使AD2=DE•DF．为什么？
 |
| AC |
点F，P为ED的延长线上一点．（1）当△PCF满足什么条件时，PC与⊙O相切．为什么？
（2）当点D在劣弧
|
| AC |
（1）当PC=PF（∠PCF=∠PFC或△PCF为等边三角形）时，PC与⊙O相切．
连接OC，则∠OCA=∠FAH
∵PC=PF
∴∠PCF=∠PFC=∠AFH
∵DE⊥AB于H
∴∠OCA+∠PCF=∠FAH+∠AFH=90°
即OC⊥PC
∴PC与⊙O相切
（2）当点D是弧AC的中点时，AD2=DE•DF．
连接AE
∵弧AD=弧CD
∴∠DAF=∠DEA
∵∠ADF=∠EDA
∴△DAF∽△DEA
∴
=
即AD2=DE•DF．
连接OC，则∠OCA=∠FAH
∵PC=PF
∴∠PCF=∠PFC=∠AFH
∵DE⊥AB于H
∴∠OCA+∠PCF=∠FAH+∠AFH=90°
即OC⊥PC
∴PC与⊙O相切
（2）当点D是弧AC的中点时，AD2=DE•DF．
连接AE
∵弧AD=弧CD
∴∠DAF=∠DEA
∵∠ADF=∠EDA
∴△DAF∽△DEA
∴
| AD |
| DE |
| DF |
| AD |
即AD2=DE•DF．
练习册系列答案
相关题目
