��Ŀ����
����Ŀ����ͼ1����һ�ž���ֽƬABCD����֪AB=10��AD=12���ֽ�ֽƬ�������²������ֽ�ֽƬ���ۺ�BF�����۵���ʹ��A����BC���ϵĵ�E������F��AD�ϣ���ͼ2����Ȼ��ֽƬ���ۺ�DH���еڶ����۵���ʹ��C���ڵ�һ�ε��ۺ�BF�ϵĵ�G������H��BC�ϣ���ͼ3���������ĸ����ۣ�
��AF�ij�Ϊ10���ڡ�BGH���ܳ�Ϊ18���� ![]() =
= ![]() ����GH�ij�Ϊ5��
����GH�ij�Ϊ5��
������ȷ�Ľ����� �� ��д��������ȷ���۵ķ��ţ�
���𰸡��٢ۢ�
���������⣺��ͼ������G��MN��AB���ֱ�AD��BC�ڵ�M��N��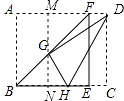
���ı���ABCDΪ���Σ�
��AB=CD=10��BC=AD=12��
���۵��ɵ�AB=BE���ҡ�A=��ABE=��BEF=90�㣬
���ı���ABEFΪ�����Σ�
��AF=AB=10��
�ʢ���ȷ��
��MN��AB��
���BNG�͡�FMGΪ����ֱ�������Σ���MN=AB=10��
��BN=x����GN=AM=x��MG=MN��GN=10��x��MD=AD��AM=12��x��
�����۵��Ŀ�֪DG=DC=10��
��Rt��MDG�У��ɹ��ɶ����ɵ�MD2+MG2=GD2 ��
����12��x��2+��10��x��2=102 �� ���x=4��
��GN=BN=4��MG=6��MD=8��
�֡�DGH=��C=��GMD=90�㣬
���NGH+��MGD=��MGD+��MDG=90�㣬
���NGH=��MDG���ҡ�DMG=��GNH��
���MGD�ס�NHG��
�� ![]() =
= ![]() =
= ![]() ����
���� ![]() =
= ![]() =
= ![]() ��
��
��NH=3��GH=CH=5��
��BH=BC��HC=12��5=7��
�ʢ���ȷ��
�֡�BNG�͡�FMGΪ����ֱ�������Σ���BN=4��MG=6��
��BG=4 ![]() ��GF=6
��GF=6 ![]() ��
��
���BGF���ܳ�=BG+GH+BH=4 ![]() +5+7=12+4
+5+7=12+4 ![]() ��
�� ![]() =
= ![]() =
= ![]() ��
��
�ʢڲ���ȷ������ȷ��
���Ͽ�֪��ȷ��Ϊ�٢ۢܣ�
���Դ��ǣ��٢ۢܣ�
�����㾫����������Ĺؼ��������ⷭ�۱任���۵����⣩�����֪ʶ�������۵���һ�ֶԳƱ任����������Գƣ��Գ����Ƕ�Ӧ������ߵĴ�ֱƽ���ߣ��۵�ǰ��ͼ�ε���״�ʹ�С���䣬λ�ñ仯����Ӧ�ߺͽ���ȣ��Լ������������ε����ʵ����⣬�˽��Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������Σ�

 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д�




