题目内容
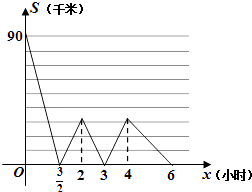
【题目】甲从M地骑摩托车匀速前往N地,同时乙从N地沿同一条公路骑自行车匀速前往M地,甲到达N地后,原路原速返回,追上乙后返回到M地.设甲、乙与N地的距离分别为y1、y2千米,甲与乙之间的距离为s千米,设乙行走的时间为x小时.y1、y2与x之间的函数图象如图1. 
(1)分别求出y1、y2与x的函数表达式;
(2)求s与x的函数表达式,并在图2中画出函数图象;
(3)当两人之间的距离不超过5千米时,能够用无线对讲机保持联系.并且规定:持续联系时间不少于15分钟为有效联系时间.求当两人用无线对讲机保持有效联系时,x的取值范围.
【答案】
(1)解:由图1知摩托车的速度为: ![]() =45(千米/小时),自行车的速度
=45(千米/小时),自行车的速度 ![]() =15(千米/小时),
=15(千米/小时),
∴点B的坐标为(2,0),点D 的坐标为(4,90),
当0≤x≤2时,y1=90﹣45x,
当2≤x≤4时,y1=45x﹣90,
y2=15x
(2)解:甲和乙在A点第一次相遇,时间t1= ![]() =1.5小时,
=1.5小时,
甲和乙在C点第二次相遇,时间t2= ![]() =3小时,.
=3小时,.
当0≤x≤1.5时,s=y1﹣y2=﹣45x+90﹣15x=﹣60x+90,
∴x=1.5时,s=0,
当1.5≤x≤2时,s=y2﹣y1=15x﹣(﹣45x+90)=60x﹣90,
∴x=2时,s=30,
当2≤x≤3时,s=y2﹣y1=15x﹣(45x﹣90)=﹣30x+90,
∴x=3时,s=0,
当3 ![]() 时,s=y1﹣y2=45x﹣90﹣15x=30x﹣90,
时,s=y1﹣y2=45x﹣90﹣15x=30x﹣90,
∴x=4时,s=30,
当4≤x≤6时,s=90﹣y2=90﹣15x,
∴x=6时,s=0,
故描出相应的点就可以补全图象.如图所示,
(3)解:∵0≤x≤1.5,s=﹣60x+90,s=5时,x= ![]() ,
,
1.5≤x≤2,s=﹣60x﹣90,s=5时,x= ![]() ,
,
2≤x≤3,s=﹣30x+90,s=5时,x= ![]() ,
,
3≤x≤4,s=30x﹣90,s=5时,x= ![]() ,
,
4≤x≤6,s=﹣1.5x+90,s=5时,x= ![]() ,
,
∴由图象知当两人距离不超过5千米时x的取值范围为:
![]() ≤x≤
≤x≤ ![]() ,
, ![]() ≤x≤
≤x≤ ![]() ,
, ![]() ≤x≤6,
≤x≤6,
60×( ![]() ﹣
﹣ ![]() )=10分钟,60×(
)=10分钟,60×( ![]() ﹣
﹣ ![]() )=20分钟,60×(6﹣
)=20分钟,60×(6﹣ ![]() )=20分钟.
)=20分钟.
∴当两人能够用无线对讲机保持有效联系时x的取值范围为:
![]() ≤x≤
≤x≤ ![]() ,
, ![]() ≤x≤6
≤x≤6
【解析】(1)先求出B、D坐标,分0≤x≤2或2≤x≤4利用待定系数法分别求出y1 , 再利用待定系数法求出y2即可.(2)分当0≤x≤1.5时,当1.5≤x≤2时,当2≤x≤3时,当3 ![]() 时,当4≤x≤6时,分别构建一次函数即可解决问题.(3)利用(2)的结论求出s=5时的x的值,再根据条件确定符合条件的x的范围.
时,当4≤x≤6时,分别构建一次函数即可解决问题.(3)利用(2)的结论求出s=5时的x的值,再根据条件确定符合条件的x的范围.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为进一步缓解城市交通压力,义乌市政府推出公共自行车,公共自行车在任何一个网店都能实现通租通还,某校学生小明统计了周六校门口停车网点各时段的借、还自行车数,以及停车点整点时刻的自行车总数(称为存量)情况,表格中x=1时的y的值表示8:00点时的存量,x=2时的y值表示9:00点时的存量…以此类推,他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
时段 | x | 还车数 | 借车数 | 存量y |
7:00﹣8:00 | 1 | 7 | 5 | 15 |
8:00﹣9:00 | 2 | 8 | 7 | n |
… | … | … | … | … |
根据所给图表信息,解决下列问题:
(1)m= , 解释m的实际意义:;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知10:00﹣11:00这个时段的借车数比还车数的一半还要多2,求此时段的借车数.