题目内容
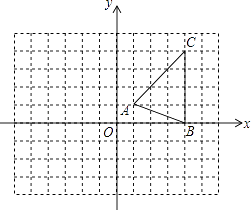
【题目】如图,在△ABD中,AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC. 
(1)求证:四边形ABCD是菱形;
(2)如果OA,OB(OA>OB)的长(单位:米)是一元二次方程x2﹣7x+12=0的两根,求AB的长以及菱形ABCD的面积;
(3)若动点M从A出发,沿AC以2m/S的速度匀速直线运动到点C,动点N从B出发,沿BD以1m/S的速度匀速直线运动到点D,当M运动到C点时运动停止.若M、N同时出发,问出发几秒钟后,△MON的面积为 ![]() ?
?
【答案】
(1)证明:∵AO平分∠BAD,AB∥CD
∴∠DAC=∠BAC=∠DCA
∴△ACD是等腰三角形,AD=DC
又∵AB=AD
∴AB=CD,
∴四边形ABCD为平行四边形,
又∵AB=AD,∴ABCD是菱形
(2)解:解方程x2﹣7x+12=0,得
OA=4,OB=3,
利用勾股定理AB= ![]() =5,
=5,
S菱形ABCD= ![]() AC×BD=
AC×BD= ![]() ×8×6=24平方米
×8×6=24平方米
(3)解:在第(2)问的条件下,设M、N同时出发x秒钟后,△MON的面积为 ![]() ,
,
当点M在OA上时,x<2,S△MON= ![]() (4﹣2x)(3﹣x)=
(4﹣2x)(3﹣x)= ![]() ;
;
解得x1= ![]() ,x2=
,x2= ![]() (大于2,舍去);
(大于2,舍去);
当点M在OC上且点N在OB上时,2<x<3,S△MON= ![]() (3﹣x)(2x﹣4)=
(3﹣x)(2x﹣4)= ![]() ,
,
解得x1=x2= ![]() ;
;
当点M在OC上且点N在OD上时,即3<x≤4,S△MON= ![]() (2x﹣4)(x﹣3)=
(2x﹣4)(x﹣3)= ![]() ;
;
解得x1= ![]() ,x2=
,x2= ![]() (小于3,舍去).
(小于3,舍去).
综上所述:M,N出发 ![]() 秒,
秒, ![]() 秒,
秒, ![]() 秒钟后,△MON的面积为
秒钟后,△MON的面积为 ![]()
【解析】(1)根据题意,用“一组对边平行且相等的四边形是平行四边形”先判定平行四边形,再用邻边相等证明菱形;(2)解方程可得OA、OB的长,用勾股定理可求AB,根据“菱形的面积对应对角线积的一半”计算连线面积;(3)根据点M、N运动过程中与O点的位置关系,分三种情况分别讨论.
【考点精析】通过灵活运用等腰三角形的性质和菱形的判定方法,掌握等腰三角形的两个底角相等(简称:等边对等角);任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形即可以解答此题.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔试 | 面试 | 体能 | |
甲 | 83 | 79 | 90 |
乙 | 85 | 80 | 75 |
丙 | 80 | 90 | 73 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.