题目内容
【题目】如图,在菱形ABCD中,E、F分别是AB和BC上的点,且BE=BF. 
(1)求证:△ADE≌△CDF;
(2)若∠A=40°,∠DEF=65°,求∠DFC的度数.
【答案】
(1)解:∵四边形ABCD是菱形,
∴∠A=∠C,AB=CB,AD=DC,
∵BE=BF,
∴AE=CF,
在△ADE和△CDF中,
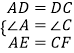
∴△ADE≌△CDF
(2)解:∵△ADE≌△CDF,
∴DE=DF,
∵∠DEF=65°,
∴∠EDB=∠FDB=25°,
∵四边形ABCD是菱形,
∴AB=AD,
∵∠A=40°,
∴∠ADB=70°,
∴∠ADE=70°﹣25°=45°,
∴∠DFC=180°﹣40°﹣45°=95°
【解析】(1)根据菱形的性质和全等三角形的判定方法“SAS”即可证明△ADE≌△CDF;(2)根据△ADE≌△CDF,得到DE=DF,再求出∠EDB=∠FDB=25°,根据四边形ABCD是菱形,∠A=40°,求出∠ADB=70°,∠ADE=45°,再根据三角形的内角和为180°,即可解答.
【考点精析】关于本题考查的菱形的性质,需要了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能得出正确答案.

练习册系列答案
相关题目







