��Ŀ����
����Ŀ������Ϊ 1����Ϊ a �ij�����ֽƬ(0.5<a<1)��ͼ�۵�������һ���߳����ڳ����εĿ��ȵ�������(��Ϊ��һ�β���)���ٰ�ʣ�µij�������ͼ�۵�������һ���߳����ڴ�ʱ�����ο��ȵ������� (��Ϊ�ڶ��β���)����˷���������ȥ����˷�����ȥ�����ڵ� n �β�����ʣ�µij�����ǡ��Ϊ�����Σ��������ֹ.

��1����һ�β�����ʣ�µij��������߳��ֱ�Ϊ ��(�ú� a �Ĵ���ʽ��ʾ)
��2�����ڶ��β�����ʣ�µij�����ǡ���������Σ����� a ��ֵ��д�������̣�
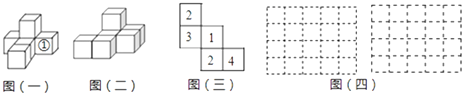
��3���������β�����ʣ�µij�����ǡ���������Σ�����ʾ��ͼ�Σ�ֱ��д�� a ��ֵ.
���𰸡���1��a �� 1-a����2��a=![]() ����3��ͼ���������a=
����3��ͼ���������a=![]() �� a=
�� a=![]() ��
��
��������
��1��������һ�β�����֪ʣ�µij�����һ�߳�Ϊa����һ�߳�Ϊ1��a��
��2�����ڶ��β�������ʣ�µij�����ǡ���������������һ�β�����ʣ�µij����εij�Ϊ����2�����ɴ˿ɵó�����a��һԪһ�η�������֮���ɵó�������
��3���������β�������ʣ�µij�����ǡ��������������ڶ��β�����ʣ�µij����εij�Ϊ����2�����ɴ˿ɵó�����a��һԪһ�η�������֮���ɵó�������
��1����һ�β�������ʣ�µij��������߳��ֱ�Ϊa����1��a����
�ʴ�Ϊ��a��1��a��
��2�����ڶ��β�������ʣ�µij�����ǡ��������������a��2��1��a����2a��1��a�������a![]() ��a
��a![]() ����ȥ����
����ȥ����
��3���������β�������ʣ�µij�����ǡ��������������ͼ��ʾ����1��a��2��2a��1����2��1��a����2a��1�������a![]() ��a
��a![]() ��
��

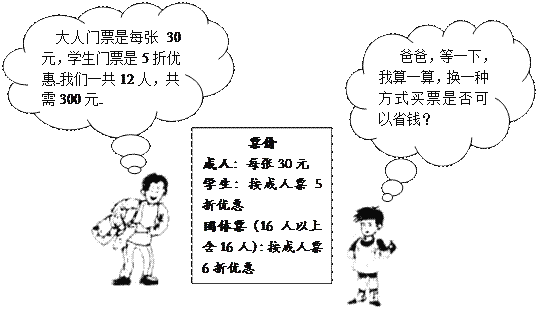
����Ŀ��ijˮ�������г�ƻ���ļ۸����±���
����ƻ�� | ������20ǧ�˵IJ��� | ����20ǧ�˵�������40ǧ�˵IJ��� | ����40ǧ�˵IJ��� |
ÿǧ�˵ļ۸� | 6Ԫ | 5Ԫ | 4Ԫ |
��1��С����һ�ι���ƻ��10ǧ�ˣ���Ҫ���Ѷ���Ԫ��
С���ڶ��ι���ƻ��![]() ǧ�ˣ�
ǧ�ˣ�![]() ����20ǧ�˵�������40ǧ�ˣ�����Ҫ���Ѷ���Ԫ���ú�
����20ǧ�˵�������40ǧ�ˣ�����Ҫ���Ѷ���Ԫ���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��2��Сǿ�����ι�����100ǧ�ˣ��ڶ��ι�����������ڵ�һ�ι�����������ҵ�һ�ι��������Ϊ![]() ǧ�ˣ�����Сǿ���ι���ƻ������Ҫ���Ѷ���Ԫ�����ú�
ǧ�ˣ�����Сǿ���ι���ƻ������Ҫ���Ѷ���Ԫ�����ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����