题目内容
【题目】某人承包了一池塘养鱼,他想估计一下收入情况.于是让他上初三的儿子帮忙.他儿子先让他从鱼塘里随意打捞上了60条鱼,把每条鱼都作上标记,放回鱼塘;过了2天,他让他父亲从鱼塘内打捞上了50条鱼,结果里面有2条带标记的.假设当时这种鱼的市面价为2.8元/斤,平均每条鱼估计2.3斤,你能帮助他估计一下今年的收入情况吗?
【答案】9660
【解析】试题分析：由最后捞出的鱼可知有标记的鱼的频率是
=
，再进一步求得池塘里鱼的总数，最后求出今年收入.
解：设池塘中共有鱼x条，
则
=
，得x=1500（条）.
则池塘中鱼的总质量为1500×2.3=3450（斤），
则今年的收入约为3450×2.8=9660（元）.
答：今年的收入约为9660元.
寒假天地重庆出版社系列答案【题目】修正后的《水污染防治法》于2018年1月1日起施行，某企业为了提高污水处理的能力，决定购买10台污水处理设备，现有
两种型号的设备，其中每台的价格、月处理污水量如下表：
|
| |
价格（万元/台） | 12 | 10 |
处理污水量（吨/月） | 240 | 200 |
经预算，该企业购买设备的资金不高于105万元.
（1）请你设计该企业可能的购买方案；
（2）若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案？请说明理由.
【题目】为了解某种车的耗油量，我们对这种车在高速公路上做了耗油试验，并把试验的数据记录下来， 制成如表：
汽车行驶时间 t（小时） | 0 | 1 | 2 | 3 | … |
油箱剩余油量 Q（升） | 100 | 94 | 88 | 82 | … |
（1）上表反映的两个变量中，自变量是 ，因变量是 ；
（2）根据上表可知，该车油箱的大小为 升，每小时耗油 升；
（3）请求出两个变量之间的关系式（用 t 来表示 Q）.
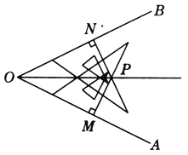
【题目】数学活动课上，同学们探究了角平分线的作法．下面给出三个同学的作法：
小红的作法
如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，再过点O作MN的垂线，垂足为P，则射线OP便是∠AOB的平分线．
小明的作法 如图，∠AOB是一个任意角，在边OA、OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合，过角尺顶点C的射线OC便是∠AOB的平分线．
|
小刚的作法 如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，再分别过点M，N作OA，OB的垂线，交点为P，则射线OP便是∠AOB的平分线．
|
请根据以上情境，解决下列问题
(1)小红的作法依据是 ．
(2)为说明小明作法是正确的，请帮助他完成证明过程．
证明：∵OM＝ON，OC＝OC， ，
∴△OMC≌△ONC( )(填推理的依据)
(3)小刚的作法正确吗?请说明理由