Question

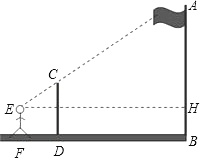
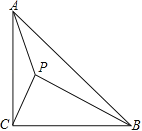
【题目】如图，某一时刻，小宁站在斜坡AC上的A处，小李在大楼FD的楼顶F处，此时小宁望小李的仰角为18．43°．5秒后，小宁沿斜坡AC前进到达C处，小李从大楼F处下楼到大楼E处，此时小李望小宁的俯角为22．6°；然后小李继续下楼，小宁沿CD前往楼底D处，已知小宁的速度为5．2米/秒，大楼FD的高度为30米，斜坡AC的坡度为1：2．4，小李、小宁都保持匀速前进，若斜坡、大楼在同一平面内，小李、小宁的身高忽略不计，则当小李达到楼底D处时，小宁距离D处的距离为（　　）米．

（已知：tan18．43°≈，sin18．43°≈，cos22．6°≈，tan22．6≈）

A.10B.15．6C.20．4D.26

Answer 1

【答案】A

【解析】

作AM⊥DF于M．解直角三角形求出EF，推出EF＝DE＝15米，推出点E运动到D的时间是5秒，由此即可解决问题．

解：作AM⊥DF于M．

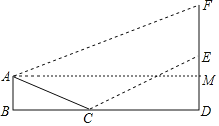
在Rt△ABC中，∵∠B＝90°，AC＝5×5．2＝26（米），AB：BC＝5：12，

∴可以假设AB＝5k，BC＝12k，

∴（5k）2+（12k）2＝262，

解得k＝2或﹣2（舍弃），

∴AB＝10（米），BC＝24（米），

∵四边形ABDM是矩形，

∴AB＝DM＝10（米），

∵DF＝30米，

∴FM＝FD﹣DM＝20（米），

∵tan∠FAM＝＝，

∴AM＝BD＝60（米），

∴CD＝BD﹣BC＝36（米），

∵tan∠ECD＝＝，

∴DE＝15（米），

∴EF＝DE，

∴点E运动到D的时间是5秒，

∴当小李达到楼底D处时，小宁距离D处的距离为36﹣5×5．2＝10（米）．

故选：A．