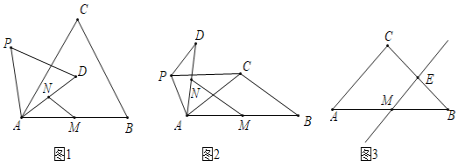
��Ŀ����
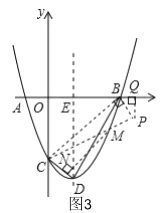
����Ŀ����ͼ����֪��������y��x2+bx+c��x�ύ��A����1��0����B��3��0�����㣬��y�ύ�ڵ�C����DΪ���㣬����BD��CD�������ߵĶԳ�����x�ύ���E��
��1���������߽���ʽ����D�����ꣻ
��2��G����������B��D֮���һ�㣬��S�ı���CDGB��4S��DGB�����G�����ꣻ
��3������������B��D֮���Ƿ����һ��M������M��MN��CD����ֱ��CD�ڵ�N��ʹ��C��M��NΪ��������������BDE���ƣ������ڣ�������������ĵ�M�����꣬�������ڣ���˵�����ɣ�
���𰸡���1��![]() ������
������![]()
![]() ����2��
����2��![]() ����3�����ڣ���
����3�����ڣ���![]() ��
��![]() ��
��
��������
��1�����ô���ϵ��������������ߵĽ���ʽ��Ȼ�ɶ���ʽ�ɵõ�D�����ꣻ
��2������BC��BG��DG���������![]() ��Ȼ�����S�ı���CDGB��4S��DGB�ɵ�
��Ȼ�����S�ı���CDGB��4S��DGB�ɵ�![]() �����ֱ��
�����ֱ��![]() �Ľ���ʽ����
�Ľ���ʽ����![]() ����H��x��2x-6��������
����H��x��2x-6��������![]() �ó����̣��ⷽ�����x���ɽ�����⣻
�ó����̣��ⷽ�����x���ɽ�����⣻
��3����ͼ3����C��M��NΪ���������������BDE���ƣ�����B��C��PΪ���������������BDE���ƣ���![]() ��
��![]() �����
�����![]() ��
��![]() ��Ȼ���
��Ȼ���![]() ��
��![]() ����������ֱ����ֱ��CP�Ľ���ʽ���ɽ�����⣮
����������ֱ����ֱ��CP�Ľ���ʽ���ɽ�����⣮
�⣺��1��![]() ������
������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬
���㣬
![]() �����
�����![]() ��
��
�������ߵĽ���ʽΪ��![]() ��
��
![]() ��
��
![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��
��2����ͼ2������![]() ��BG��DG��
��BG��DG��
��![]() ����
����![]() ����
����![]() ��
��
���![]() ��
��
������ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��ֱ��![]() ��Գ����ཻ�ڵ�
��Գ����ཻ�ڵ�![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
���![]() ��
��
��![]() ��
��
![]() ��
��
![]() �ı���
�ı���![]() ��
��
![]() ��
��
�����![]() ��
��![]() ��ƽ�е�ֱ�߽�BD�ڵ�
��ƽ�е�ֱ�߽�BD�ڵ�![]() ��ֱ��
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��![]() �����
�����![]() ��
��
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��![]() ����H��x��2x-6����
����H��x��2x-6����
��![]() ��
��
��![]() ��
��
�����ã�![]() ��
��
��ã�![]() ����
����![]() ��
��
���![]() ��
��
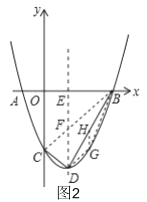
��3�����ڣ�
�ɹ��ɶ����ã�![]() ��
��
��ͼ3������![]() ��
��![]() ��
��![]() ���ӳ�����
���ӳ�����![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��ļнǶ���
��ļнǶ���![]() ��
��
![]() ��
��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() �������������
Ϊ�������������![]() ���ƣ�
���ƣ�
![]() ��
��![]() ��
��![]() ��
��![]() �������������
Ϊ�������������![]() ���ƣ�
���ƣ�
![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��ã�![]() ��
��![]() ��
��
����![]() ��
��![]() ����
����![]() ��
��
![]() ��
��
![]() ��
��
�ٵ�![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
���![]() ��
��
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��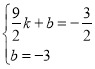 �����
�����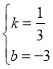 ��
��
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
����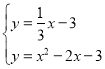 ����ã�
����ã�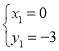 ����ȥ����
����ȥ����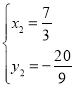 ��
��
���![]() ��
��
�ڵ�![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
���![]() ��
��
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��![]() �����
�����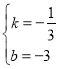 ��
��
��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
����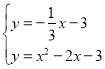 �����
����� ����ȥ����
����ȥ���� ��
��
![]() ��
��![]() ��
��
�������������ڵ�![]() ��
��![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��![]() �������������
Ϊ�������������![]() ���ƣ�
���ƣ�

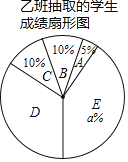
����Ŀ����ѧ����ǰ��ij������ʦΪ���˽����ν̵ļס�������ѧ������������Ļ���֪ʶ������������������ѧ�����������Ļ���֪ʶ���м�⣬����100�֣��ִ�������ֱ������ȡ��20��ѧ���ļ��ɼ����������������ͷ������ɼ��÷���x��ʾ������Ϊ���飺
A.0��x��80��B.80��x��85��C.85��x��90��D.90��x��95��E.95��x��100������������˲�����Ϣ��
�װ�20��ѧ���ijɼ�Ϊ��
���� | 82 | 85 | 96 | 73 | 91 | 99 | 87 | 91 | 86 | 91 |
87 | 94 | 89 | 96 | 96 | 91 | 100 | 93 | 94 | 99 |
�Ұ�20��ѧ���ijɼ���D���е������ǣ�93��91��92��94��92��92��92
�ס��������ȡ��ѧ���ɼ�����ͳ�Ʊ�
�༶ | ���� | ���� |
ƽ���� | 91 | 92 |
��� | 91 | b |
���� | c | 92 |
���� | 41.2 | 27.3 |
����������Ϣ������������⣺
��1��ֱ��д������ͼ����a��b��c��ֵ��a���� ����b���� ����c���� ����
��2�������������ݣ�����Ϊ�ס������������ĸ����ѧ������֪ʶ��������Ϻã���˵�����ɣ�һ�����ɼ��ɣ���
��3�����ס�������������Ϊ125���Ҷ��μ��˴˴λ���֪ʶ��⣬���ƴ˴μ��ɼ����㣨x��95����ѧ�������Ƕ��٣�