题目内容
【题目】已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求这条抛物线的解析式;
求这条抛物线的解析式;
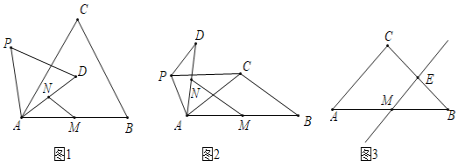
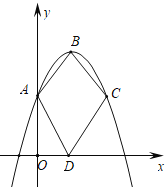
![]() 如图1,点P是第三象限内抛物线上的一个动点,当四边形
如图1,点P是第三象限内抛物线上的一个动点,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
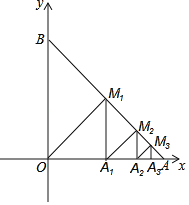
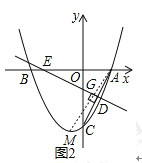
![]() 如图2,线段
如图2,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,垂足为
,垂足为![]() 为抛物线的顶点,在直线
为抛物线的顶点,在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1) ![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]()
【解析】
(1) 用待定系数法即可得到答案;
(2)连接![]() ,设点
,设点![]() ,由题意得到
,由题意得到![]()
![]() .即可得到答案.
.即可得到答案.
(3)用待定系数法求解析式,再结合勾股定理即可得到答案.
解:![]() 抛物线
抛物线![]() 经过点
经过点![]() ,
,
![]() ,
,
解得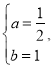
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
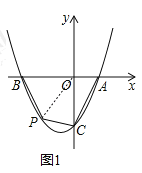
![]() 如图1,连接
如图1,连接![]() ,设点
,设点![]() ,其中
,其中![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,由题意得
,由题意得![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,开口向下,
,开口向下,![]() 有最大值,
有最大值,
![]() 当
当![]() 时,四边形
时,四边形![]() 的面积最大,
的面积最大,
此时,![]() ,即
,即![]() .
.
因此当四边形![]() 的面积最大时,点
的面积最大时,点![]() 的坐标为
的坐标为![]() .
.
![]()
![]() ,
,
![]() 顶点
顶点![]() .
.
如图2,连接![]() 交直线
交直线![]() 于点
于点![]() ,此时,
,此时,![]() 的周长最小.
的周长最小.
设直线![]() 的解析式为
的解析式为![]() ,且过点
,且过点![]() ,
,![]() ,
,
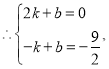
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
在![]() 中,
中,![]() .
.
![]() 为
为![]() 的中点,
的中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
由图可知![]()
设直线![]() 的函数解析式为
的函数解析式为![]() ,
,
![]()
解得: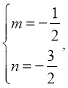
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
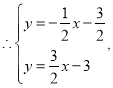
解得:
![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】入学考试前,某语文老师为了了解所任教的甲、乙两班学生假期向的语文基础知识背诵情况,对两个班的学生进行了语文基础知识背诵检测,满分100分.现从两个班分别随机抽取了20名学生的检测成绩进行整理,描述和分析(成绩得分用x表示,共分为五组:
A.0≤x<80,B.80≤x<85,C.85≤x<90,D.90≤x<95,E.95≤x<100),下面给出了部分信息:
甲班20名学生的成绩为:
甲组 | 82 | 85 | 96 | 73 | 91 | 99 | 87 | 91 | 86 | 91 |
87 | 94 | 89 | 96 | 96 | 91 | 100 | 93 | 94 | 99 |
乙班20名学生的成绩在D组中的数据是:93,91,92,94,92,92,92
甲、乙两班抽取的学生成绩数据统计表
班级 | 甲组 | 乙组 |
平均数 | 91 | 92 |
中位数 | 91 | b |
众数 | c | 92 |
方差 | 41.2 | 27.3 |
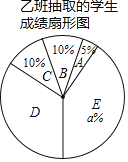
根据以上信息,解答下列问题:
(1)直接写出上述图表中a,b,c的值:a= ;b= ;c= ;
(2)根据以上数据,你认为甲、乙两个班中哪个班的学生基础知识背诵情况较好?请说明理由(一条理由即可);
(3)若甲、乙两班总人数为125,且都参加了此次基础知识检测,估计此次检测成绩优秀(x≥95)的学生人数是多少?