��Ŀ����
����Ŀ�����꼶����ʦ��ѧС�龭���г����ˣ��õ�ij���˶�����������y���������ۼ�x��Ԫ/������һ�κ��������ۼۡ���������������������w��Ԫ���������Ӧֵ�����
�ۼ�x��Ԫ/���� | 130 | 150 | 180 |
��������y������ | 210 | 150 | 60 |
����������w��Ԫ�� | 10500 | 10500 | 6000 |
ע�������������������������ۼ۩����ۣ�
��1����y����x�ĺ�������ʽ����Ҫ��д���Ա�����ȡֵ��Χ����
��2���˶����Ľ������� ��Ԫ/����
��3�����ۼ��Ƕ���ʱ�����������������������Ƕ���Ԫ��
���𰸡���1��y����3x+600����2��80����3�����ۼ���140Ԫʱ����������������������Ϊ10800Ԫ
��������
��1����y����x�ĺ�������ʽΪ��y=kx+b��k��0�����������������ݵö�Ԫһ�η����飬���k��b��ֵ�ٴ���y=kx+b���ɣ�
��2���˶����Ľ��۵����ۼۼ�ȥÿ��������
��3������ÿ��������������������������������ù���x�Ķ��κ������䷽�����ݶ��κ��������ʿɵô𰸣�
��1����y����x�ĺ�������ʽΪ��y��kx+b��k��0��
������ã�![]()
��ã�![]()
��y����x�ĺ�������ʽΪy����3x+600��
��2���˶����Ľ����ǣ�130��10500��210��80��Ԫ��
�ʴ�Ϊ��80��
��3������������w����x��80������3x+600��
����3x2+840x��48000
����3��x��140��2+10800
�൱�ۼ���140Ԫʱ����������������������Ϊ10800Ԫ��

 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�����Ŀ����ѧ����ǰ��ij������ʦΪ���˽����ν̵ļס�������ѧ������������Ļ���֪ʶ������������������ѧ�����������Ļ���֪ʶ���м�⣬����100�֣��ִ�������ֱ������ȡ��20��ѧ���ļ��ɼ����������������ͷ������ɼ��÷���x��ʾ������Ϊ���飺
A.0��x��80��B.80��x��85��C.85��x��90��D.90��x��95��E.95��x��100������������˲�����Ϣ��
�װ�20��ѧ���ijɼ�Ϊ��
���� | 82 | 85 | 96 | 73 | 91 | 99 | 87 | 91 | 86 | 91 |
87 | 94 | 89 | 96 | 96 | 91 | 100 | 93 | 94 | 99 |
�Ұ�20��ѧ���ijɼ���D���е������ǣ�93��91��92��94��92��92��92
�ס��������ȡ��ѧ���ɼ�����ͳ�Ʊ�
�༶ | ���� | ���� |
ƽ���� | 91 | 92 |
��� | 91 | b |
���� | c | 92 |
���� | 41.2 | 27.3 |
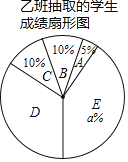
����������Ϣ������������⣺
��1��ֱ��д������ͼ����a��b��c��ֵ��a���� ����b���� ����c���� ����
��2�������������ݣ�����Ϊ�ס������������ĸ����ѧ������֪ʶ��������Ϻã���˵�����ɣ�һ�����ɼ��ɣ���
��3�����ס�������������Ϊ125���Ҷ��μ��˴˴λ���֪ʶ��⣬���ƴ˴μ��ɼ����㣨x��95����ѧ�������Ƕ��٣�