题目内容
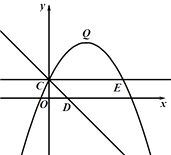
【题目】如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，且经A（1，0）、B（0，﹣3）两点．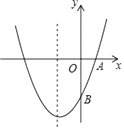
（1）求抛物线的解析式；
（2）在抛物线的对称轴x=﹣1上，是否存在点M，使它到点A的距离与到点B的距离之和最小，如果存在求出点M的坐标，如果不存在请说明理由．
【答案】
（1）解：根据题意得：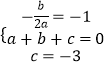 
，解得： 
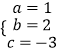，则二次函数的解析式是y=x2+2x﹣3；
（2）解：存在．设抛物线与x轴的另一个交点是C，由抛物线的对称性得BC与对称轴的交点就是M．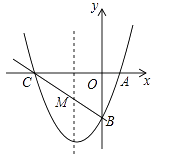
∵C点的坐标是（﹣3，0），设直线BC的解析式是y=kx﹣3，则0=﹣3k﹣3，解得k=﹣1，∴直线BC的解析式是y=﹣x﹣3．
当x=﹣1时，y=﹣2，
∴点M的坐标是（﹣1，﹣2）．
【解析】（1）利用待定系数法，由对称轴公式x=
， 把A、B坐标代入解析式，得出方程组，解方程组，求出解析式；（2）求两线段之和最小，常利用对称法，找出定点关于定直线的对称点，连接对称点和另一点与定直线相交，可找出最短位置.
【考点精析】认真审题，首先需要了解轴对称-最短路线问题(已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径)．
练习册系列答案
相关题目
