��Ŀ����
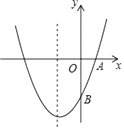
����Ŀ����ͼ�������� ![]() ��ͼ�����C��0��1��������ΪQ��2��3��,��D��x���������ϣ��߶�OD=OC.
��ͼ�����C��0��1��������ΪQ��2��3��,��D��x���������ϣ��߶�OD=OC.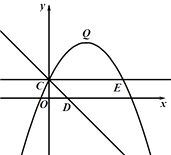
��1���������ߵĽ���ʽ��
��2�����������Ƿ���ڵ�M��ʹ�á�CDM����CDΪֱ�DZߵ�ֱ�������Σ������ڣ������M������ꣻ�������ڣ���˵�����ɣ�
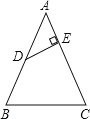
��3����ֱ��CD�Ƶ�C��ʱ�뷽����ת45������ֱ�����������ཻ����һ��E������QE.����P���߶�QE�ϵĶ��㣬��F���߶�OD�ϵĶ��㣬�ʣ���P���F����ƶ������У���PCF���ܳ��Ƿ������Сֵ�������ڣ���������Сֵ���������ڣ���˵������.
���𰸡�
��1���⣺�������ߵĽ���ʽΪ ![]() ��
��
��C��0��1������ã� ![]() ��
��
���: ![]() ,
,
�������ߵĽ���ʽΪ�� ![]() ��
�� ![]()
��2����: ����ͼ1������CΪֱ�Ƕ���ʱ��
�ߵ�C������Ϊ��0��1����
��OD=OC=1��
���D��������1��0����
��ֱ��CDΪ ![]() ����
���� ![]() �����
����� ![]() ��
��
��ֱ��CD�Ľ���ʽΪ�� ![]() ��
��
�ߴ�ʱCM��CD��
��CM�Ľ���ʽΪ�� ![]() ��
��
�ɣ� 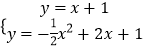 ����ã�
����ã� ![]() ��
�� ![]() ��
��
�ߵ㣨0��1�����C�غϣ�
���M������Ϊ��2��3������ʱ��M���Q�غϣ�
����ͼ�ڣ���DΪֱ�Ƕ���ʱ���ɢٿɵ�ֱ��DM�Ľ���ʽΪ ![]() ��
��
�ɣ�  ,��ã�
,��ã� ![]() ��
�� ![]() ��
��
���͵�����ΪΪ ![]() ��
�� ![]() ��
��
������������������ģ������㣬�ֱ���(2 , 3 )�� ![]() ��
�� ![]() .
.
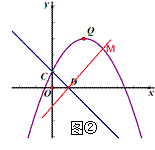
��3���⣺���ڣ���ͼ����ʾ������C����ֱ��QE�ĶԳƵ�C�䣬����C����x��ĶԳƵ�C�壬����C��C�壬��OD�ڵ�F����QE�ڵ�P�����PCF��Ϊ����������ܳ���С�������Σ�����ԳƵ����ʿ�֪����PCF���ܳ������߶�C��C��ij��ȣ�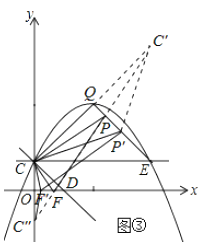
���ͼ����ʾ������C��E��
�ɣ�2����֪��QC��CD�� ������ɵã�QC=QE��
�ߡ�DCE=45�㣬
���QCE=45��=��QEC��
���QCE�ǵ���ֱ�������Σ�
��C��C�����ֱ��QE�Գƣ�
���QC��EΪ����ֱ�������Σ�
���CEC��Ϊ����ֱ�������Σ�
���������� ![]() ����
���� ![]() ���
��� ![]() ��
��
���E��������4��1����
��CE=4=C��E��
���C���������4��5����
��C��C�����x��Գƣ�
���C���������0����1����
��OC��=1��
����C����C��N��y���ڵ�N����NC��=CE=4��NC��=4+1+1=6��
��Rt��C��NC���У��ɹ��ɶ����ã�C��C��= ![]() ��
��
������������P���F���ƶ������У���PCF���ܳ�������Сֵ����СֵΪ ![]() ��
��
����������1������ʽ����Ϊ����ʽ���ٰ�C��0��1���������ʽ���ɣ���2����CDΪֱ�DZߵ�ֱ�������η�Ϊ���࣬�ֱ���C��DΪֱ�Ƕ��㣬�ɹ�C��D�ֱ���CD�Ĵ��ߣ����������ཻ������ֱ�ߺ������߽���ʽ��ɷ����飬�����M���ꣻ��3�������öԳƷ�����C���ڶ�ֱ��QE�ĶԳƵ�C'������y��ԳƵ�ΪC",�ѡ�PCF���ܳ�ת��ΪFC"+FP+PC',��C"��F��P��C'�ĵ㹲��ʱ���ܳ���С.