题目内容
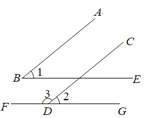
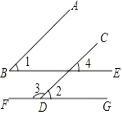
【题目】如图,已知 AB∥CD,BE∥FG.
(1)如果∠1=53°,求∠2和∠3的度数;
(2)本题隐含着一个规律,请你根据(1)的结果进行归纳,如果一个角的两边分别平行于另一个角的两边,那么这两个角__________;
(3)利用(2)的结论解答:如果两个角的两边分别平行,其中一个角比另一个角的 2倍小 30°,求这两个角的度数.
【答案】(1)∠2=53°,∠3=127°;(2)相等或互补;(3)70°,110°或30°,30°.
【解析】
(1)先根据平行线的性质求出∠4的度数,再由BE∥FG即可得出∠2的度数,根据补角的定义即可得出结论;
(2)根据(1)中的规律即可得出结论;
(3)设一个角的度数为x,则x+(2x-30°)=180°或x=2x-30,求出x的值即可.
解:(1)∵AB//CD,∠1=53°,
∴∠4=∠1=53°,
∵BE//FG,
∴∠2=∠4=53°,
∴∠3=180°-53°=127°,
(2)由(1)中的规律可知,如果两个角的两边分别平行,那么这两个角相等或互补;
故答案为:相等或互补
(3)设一个角的度数为x,则x+(2x-30°)=180°或x=2x-30,
解得:x=70°或30°,
∴这两个角的度数分别是70°,110°或30°,30°.

练习册系列答案
相关题目