题目内容
【题目】如图,两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起,∠DEA=∠ACB=90°,∠DAE=∠ABC=30°,E、A、C三点在一条直线上,连接BD,取BD中点M,连接ME、MC,试判断△EMC的形状,并说明理由.
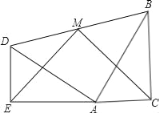
【答案】△EMC的形状是等腰直角三角形,理由见解析;
【解析】
△EMC的形状是等腰直角三角形,求出∠DAB=90°,AD=AB,推出AM⊥BD,AM=BM=DM,求出∠MBC=∠MAE,BM=AM,证△BCM≌△AEM,推出EM=CM,∠3=∠2,求出∠1+∠3=90°即可.
△EMC的形状是等腰直角三角形,
理由是:
连接AM,
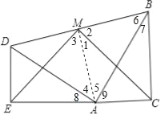
∵∠8=30°,∠9=60°,
∴∠DAB=180°﹣30°﹣60°=90°,
∵M为BD中点,AD=AB(已知两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起),
∴AM⊥BD(等腰三角形底边的高也平分底边),
AM=BM=DM(直角三角形斜边上中线等于斜边的一半),
∴∠5=∠6=![]() (180°﹣90°)=45°,∠4=∠BDA=45°,
(180°﹣90°)=45°,∠4=∠BDA=45°,
∵∠7=30°,
∴∠MBC=45°+30°=75°,
同理∠MAE=75°=∠MBC,
在△BCM和△AEM中,
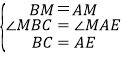 ,
,
∴△BCM≌△AEM(SAS),
∴EM=CM,∠3=∠2,
∵AM⊥BD,
∴∠1+∠2=90°,
∴∠1+∠3=90°,
∴△EMC是等腰直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目