题目内容
【题目】如图,在△ABC中,∠C=90°,AC=4,BC=3,点P从点A出发,以每秒4个单位长度的速度沿折线AC-CB运动,到点B停止.当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交AB 于点Q,再以PQ为斜边作等腰直角三角形△PQR,且点R与△ABC的另一条直角边始终在PQ同侧,设△PQR与△ABC重叠部分图形的面积为S(平方单位).点P的运动时间为t(秒).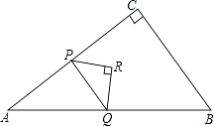
(1)求点P在AC边上时PQ的长,(用含t的代数式表示);
(2)求点R到AC、PQ所在直线的距离相等时t的取值范围;
(3)当点P在AC边上运动时,求S与t之间的函数关系式;
(4)直接写出点R落在△ABC高线上时t的值.
【答案】
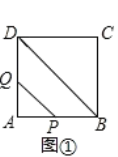
(1)解:如图①,

由题意可知AP=4t,
tanA= ![]() ,
,
∴PQ=3t;
(2)解:①当点P在AC边上时,如图①.

∵∠RPQ=45°,∠CPQ=90°,
∴∠CPR=45°=∠RPQ,
∴点R到直线AC、PQ距离相等,
此时0<t<1.
②当点P在BC边上时,过点R作RH⊥PQ于点H,如图②,

则有PC=4t-4,PB=7-4t,
∵tanB= ![]() ,
,
∴PQ= ![]() PB=
PB= ![]() (7-4t).
(7-4t).
由题可得:RH= ![]() PC.
PC.
∵RH= ![]() PQ,
PQ,
∴PC=PQ,
∴4t-4= ![]() (7-4t),
(7-4t),
解得:t= ![]() .
.
综上所述:0<t<1或t= ![]() ;
;
(3)解:①当0<t≤ ![]() 时,如图①.
时,如图①.

过点R作RH⊥PQ于点H,
S= ![]() PQRH=
PQRH= ![]() ×3t×
×3t× ![]() =
= ![]() t2.
t2.
②当 ![]() <t<1时,如图③.
<t<1时,如图③.

过点R作RH⊥PQ于点H,交BC于点G,
则有RG⊥MN,RH= ![]() PQ=
PQ= ![]() t,GH=PC=4-4t,
t,GH=PC=4-4t,
∴S=S△RPQ-S△RMN= ![]() PQRH-
PQRH- ![]() MNRH
MNRH
=RH2RG2=( ![]() t)2-[
t)2-[ ![]() t-(4-4t)]2
t-(4-4t)]2
=-28t2+44t-16;
(4)解:点R落在△ABC高线上时,t的值为 ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
可分以下几种情况讨论:如图④~⑦
①点P在AC上,且点R在AB的高CH上,如图④,

过点P作PG⊥CH于G,
易证△PGR≌△RHQ,则有PG=RH,GR=QH.
易求得AB=5,CH= ![]() ,AH=
,AH= ![]() ,BH=
,BH= ![]() .
.
PC=4-4t,CG= ![]() PC=
PC= ![]() (4-4t),PG=
(4-4t),PG= ![]() PC=
PC= ![]() (4-4t),
(4-4t),
AQ= ![]() AP=5t,QH=AH-AQ=
AP=5t,QH=AH-AQ= ![]() -5t.
-5t.
根据CH=CG+GR+RH=CG+QH+PG= ![]() ,得
,得
![]() (4-4t)+
(4-4t)+ ![]() -5t+
-5t+ ![]() (4-4t)=
(4-4t)= ![]() ,
,
解得:t= ![]() .
.
②点P在AC上,且点R在AC的高BC上,如图⑤

过点R作RH⊥PQ于H,
易得PQ=2RH=2PC,PQ= ![]() AP=3t,PC=4-4t,
AP=3t,PC=4-4t,
∴3t=2(4-4t),
解得:t= ![]() .
.
③点P在BC上,且点R在BC的高AC上,如图⑥,

过点R作RH⊥PQ于H,
易得PQ=2RH=2PC,PQ= ![]() PB=
PB= ![]() (7-4t),PC=4t-4,
(7-4t),PC=4t-4,
∴ ![]() (7-4t)=2(4t-4),
(7-4t)=2(4t-4),
解得:t= ![]() .
.
④点P在BC上,且点R在AB的高CH上,如图⑦,

过点P作PG⊥CH于G,
易证△PGR≌△RHQ,则有PG=RH,GR=QH.
易证△CGP∽△CHB,
∴ ![]() .
.
∵BC=3,CH= ![]() ,BH=
,BH= ![]() ,CP=4t-4,
,CP=4t-4,
∴CG= ![]() PC=
PC= ![]() (4t-4),PG=
(4t-4),PG= ![]() PC=
PC= ![]() (4t-4),
(4t-4),
同理可得QB= ![]() PB=
PB= ![]() (7-4t),QH=QB-BH=
(7-4t),QH=QB-BH= ![]() (7-4t)-
(7-4t)- ![]() .
.
根据CH=CG+GH=CG+RH-RG=CG+PG-QH= ![]() ,得
,得
![]() (4t-4)+
(4t-4)+ ![]() (4t-4)-[
(4t-4)-[ ![]() (7-4t)-
(7-4t)- ![]() ]=
]= ![]() ,
,
解得:t= ![]() .
.
【解析】(1)根据题意求出tanA的值,得到点P在AC边上时PQ的长;(2)①当点P在AC边上时,得到点R到直线AC、PQ距离相等,此时0<t<1;②当点P在BC边上时,由tanB的值求出PQ的代数式,点R到AC、PQ所在直线的距离相等时t的取值范围;(3)根据三角形的面积公式得到点P在AC边上运动时,S与t之间的函数关系式;(4)①点P在AC上,且点R在AB的高CH上,得到△PGR≌△RHQ,根据全等三角形的对应边相等,得到PG=RH,GR=QH;求出t的值;②点P在AC上,且点R在AC的高BC上时,求出t的值;③点P在BC上,且点R在BC的高AC上时,直接求出t的值;④点P在BC上,且点R在AB的高CH上时,得到△CGP∽△CHB,得到比例,求出t的值;此题是综合题,难度较大,计算和解方程时需认真仔细.
【考点精析】根据题目的已知条件,利用相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案