题目内容
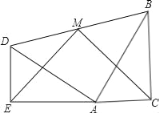
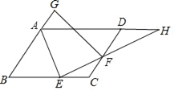
【题目】如图所示,在ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD于F.
(1)求证:CE=CF;
(2)延长AD、EF交于点H,延长BA到G,使AG=CF,若AD=7,DF=3,EH=2AE,求GF的长.
【答案】(1)见解析;(2)GF=4![]() .
.
【解析】
(1)由题意可得:∠DAE=∠BAE=∠AEB=![]() ∠BAD=
∠BAD=![]() ∠C,则
∠C,则![]() ∠C+∠FEC=90°,根据三角形内角和可得
∠C+∠FEC=90°,根据三角形内角和可得![]() ∠C+∠EFC=90°,则∠CEF=∠CFE,即可得结论;
∠C+∠EFC=90°,则∠CEF=∠CFE,即可得结论;
(2)连接AC,作AP⊥BC于P,由题意可求AB=BE=CD=5,CE=CF=2,即可求DH=3,根据勾股定理可求AE的长,根据勾股定理可列出方程,可求出 BP,AP,PE,PC的长度,再根据勾股定理可求AC的长,由题意可证AC=GF,即可得GF的长.
(1)∵四边形ABCD是平行四边形,
∴∠BAD=∠C,AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠DAB,
∴∠BAE=∠DAE=![]() ∠BAD,
∠BAD,
∴∠BAE=∠AEB=![]() ∠BAD,
∠BAD,
∴AB=BE,
∵AE⊥EF,
∴∠AEF=90°,
∴∠AEB+∠FEC=90°,即![]() ∠BAD+∠FEC=90°,
∠BAD+∠FEC=90°,
∴![]() ∠C+∠FEC=90°,
∠C+∠FEC=90°,
∵∠C+∠FEC+∠EFC=180°,
∴![]() ∠C+∠EFC=90°,
∠C+∠EFC=90°,
∴∠EFC=∠FEC,
∴CE=CF;
(2)如图连接AC,作AP⊥BC于P,
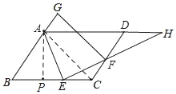
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC=7,AB∥CD,
∵CE=CF,
∴BC﹣BE=CD﹣DF,且AB=BE=CD,
∴7﹣AB=AB﹣3,
∴AB=5=BE=CD,
∴CE=CF=2,
∵AD∥BC,
∴∠H=∠FEC,且∠FEC=∠EFC,∠DFH=∠EFC,
∴∠H=∠DFH,
∴DH=DF=3,
∴AH=10,
在Rt△AEH中,AH2=AE2+EH2,且EH=2AE,
∴5AE2=100,
∴AE=2![]() ,
,
在Rt△ABP和Rt△APE中,
AP2=AB2﹣BP2,AP2=AE2﹣PE2.
∴AB2﹣BP2=AE2﹣PE2.
∴25﹣BP2=20﹣(5﹣BP)2.
∴BP=3,
∴AP=4,PE=2,PC=4,
在Rt△APC中,AC=![]() =4
=4![]() ,
,
∵AB∥CD,AG=CF,
∴四边形AGFC是平行四边形,
∴GF=AC=4![]() .
.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案【题目】我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | 6.7 | m | 3.41 | 90% | n |
八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |

(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.