题目内容
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a+b=0,④b2﹣4ac>0,其中正确结论个数是( )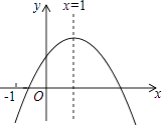
A.1
B.2
C.3
D.4
【答案】D
【解析】解:开口向下,a<0,抛物线与y轴交于正半轴,c>0,根据对称轴为x=﹣ ![]() >0,则b>0,所以abc<0,①正确;
>0,则b>0,所以abc<0,①正确;
根据x=﹣1时y<0,所以a﹣b+c<0,②正确;
根据对称轴为x=1,即﹣ ![]() =1,2a+b=0,③正确;
=1,2a+b=0,③正确;
由抛物线与x轴有两个交点,所以b2﹣4ac>0,④正确
所以答案是:D
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目