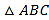题目内容
【题目】如图，直线y=﹣ 
x+6分别交x轴、y轴于A、B两点，抛物线y=﹣ 
x2+8，与y轴交于点D，点P是抛物线在第一象限部分上的一动点，过点P作PC⊥x轴于点C．
（1）点A的坐标为 ， 点D的坐标为；
（2）探究发现：
①假设P与点D重合，则PB+PC=；（直接填写答案）
②试判断：对于任意一点P，PB+PC的值是否为定值？并说明理由；
（3）试判断△PAB的面积是否存在最大值？若存在，求出最大值，并求出此时点P的坐标；若不存在，说明理由．
【答案】
（1）（4,0）,（0,8）
（2）PB+PC=10,是,理由如下：过点P作PQ⊥y轴于点Q,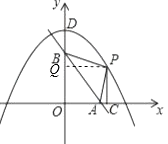
∵P在抛物线上,且在第一象限,∴设P点坐标为（x,﹣ 
x2+8）．则PQ=x,PC=﹣ x2+8．当4≤x＜8时,PB= 
= x2+2,∴PB+PC= x2+2+（﹣ x2）+8=10,当0＜x＜4时,同理可得；
（3）△PAB的面积存在最大值，且最大值为13，此时点P的坐标为（6， 
）
解：存在．
设△PAB的面积为S．
由（2）假设．
当4≤x＜8时，有S= 
=﹣ 
x2+3x+4=﹣ （x﹣6）2+13．
当0＜x＜4时，s=﹣ （x﹣6）2+13．
当x=6时，S最大=13，y=﹣ ×36+8= ，
∴△PAB的面积存在最大值，且最大值为13，此时点P的坐标为（6， ）
【解析】
解：（1）y=﹣ 
x+6当y=0时，x=4，即A（4，0），
y=﹣ x2+8当x=0时，y=8，即D点坐标（0，8），
所以答案是：（4，0），（0，8）；（2）①PB=PO﹣OB=8﹣6=2，PB+PC=8+2=10；
【题目】我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛，计分采用10分制，选手得分均为整数，成绩达到6分或6分以上为合格，达到9分或10分为优秀．这次竞赛后，七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下，其中七年级代表队得6分、10分的选手人数分别为a，b．
队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | 6.7 | m | 3.41 | 90% | n |
八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
（1）请依据图表中的数据，求a，b的值；
（2）直接写出表中的m，n的值；
（3）有人说七年级的合格率、优秀率均高于八年级，所以七年级队成绩比八年级队好，但也有人说八年级队成绩比七年级队好．请你给出两条支持八年级队成绩好的理由．
