题目内容
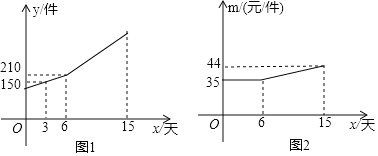
【题目】小王从同事小李手中接收一批生产任务，派单方要求必须在15天内完成，届时承以每件60元的价格全部回收，小王在接受任务之后，其生产的任务y（件）与生产的天数x（天）关系如图1所示，其中在生产6天之后，每天的生产数量达到了30件．
（1）求y与x之间的函数表达式；
（2）设第x天生产的产品成本为m元/件，m与x的函数图象如图2所示，若小王第x天的利润为W元，求W与x的关系式，并求出第几天后小王的利润可达到最大值，最大值为多少？
【答案】（1）
；（2）当1≤x≤6时，W1＝500x+2250（1≤x≤6）；当6＜x≤15时，W2＝﹣30（x﹣15）2+7680（6＜x≤15）；第15天后小王的利润可达到最大值，最大值为7680．
【解析】
（1）分当1≤x≤6、6＜x≤15时，分别求解即可；
（2）分1≤x≤6、6＜x≤15，分别求解即可．
解：（1）①当1≤x≤6时，设函数的表达式为：y＝kx+b，
由题意得：
，解得：
，
y1＝20x+90（1≤x≤6）；
②当6＜x≤15时，同理可得：y2＝30x+30（6＜x≤15）；
故函数的表达式为：y＝
；
（2）①当1≤x≤6时，m1＝35，
②当6＜x≤15时，同理可得：m2＝x+29（6＜x≤15），
故m＝
；
故当1≤x≤6时，
每件产品的利润为60﹣35＝25，
总利润W1＝25（20x+90）＝500x+2250（1≤x≤6）；
当6＜x≤15时，
每件产品的利润为60﹣（x+29）＝﹣x+31，
W2＝（30x+30）（﹣x+31）＝﹣30（x﹣15）2+7680（6＜x≤15），
故当x＝15时，函数有最大值7680，
故：第15天后小王的利润可达到最大值，最大值为7680．
练习册系列答案
相关题目
