题目内容
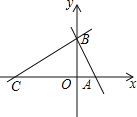
【题目】如图,平面直角坐标系中,直线y=-![]() x+
x+![]() 与坐标轴分别交于点A、B,且点C在x轴负半轴上,且AB:AC=1:2.
与坐标轴分别交于点A、B,且点C在x轴负半轴上,且AB:AC=1:2.
(1)求A、C两点的坐标;
(2)若点M从点C出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.
【答案】(1)A(1,0),C(-3,0);(2)s=2![]() -t(0≤t<2
-t(0≤t<2![]() );s==t-2
);s==t-2![]() (t>2
(t>2![]() );(3) Q坐标为(1,2)、(1,-2)、(1,
);(3) Q坐标为(1,2)、(1,-2)、(1,![]() )、(-1,0).
)、(-1,0).
【解析】
(1)由直线解析式容易求出点A的坐标,由勾股定理求出AB,再求出AC、得出OC,即可得出点C的坐标;
(2)先求出∠ABC=90°,分两种情况考虑:当M在线段BC上;当M在线段BC延长线上;表示出BM,利用三角形面积公式分别表示出S与t的函数关系式即可;
(3)点P是y轴上的点,在坐标平面内存在点Q,使以A、B、P、Q为顶点的四边形是菱形,分两种情况,利用菱形的性质求出AQ的长,根据AQ与y轴平行得到Q与A横坐标相同,求出满足题意Q得坐标即可.
(1)对于直线y=-![]() x+
x+![]() ,当y=0时,-
,当y=0时,-![]() x+
x+![]() =0,
=0,
解得:x=1,
∴A的坐标为(1,0),
∴OA=1;
当x=0时,y=![]() ,
,
∴B(0,![]() ),
),
∴OB=![]() ;
;
∵∠AOB=90°,
∴AB=![]() =2,
=2,
∵AB:AC=1:2,
∴AC=4,
∴OC=3,
∴点C的坐标为(-3,0);
(2)如图1所示:
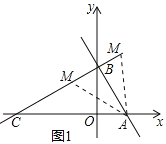
∵OA=1,OB=![]() ,AB=2,
,AB=2,
∴∠ABO=30°,
同理:BC=2![]() ,∠OCB=30°,
,∠OCB=30°,
∴∠OBC=60°,
∴∠ABC=90°,
分两种情况考虑:①若M在线段BC上时,BC=2![]() ,CM=t,则BM=BC-CM=2
,CM=t,则BM=BC-CM=2![]() -t,
-t,
此时S△ABM=![]() BMAB=
BMAB=![]() ×(2
×(2![]() -t)×2=2
-t)×2=2![]() -t(0≤t<2
-t(0≤t<2![]() );
);
②若M在BC延长线上时,BC=2![]() ,CM=t,则BM=CM-BC=t-2
,CM=t,则BM=CM-BC=t-2![]() ,
,
此时S△ABM=![]() BMAB=
BMAB=![]() ×(t-2
×(t-2![]() )×2=t-2
)×2=t-2![]() (t>2
(t>2![]() );
);
(3)P是y轴上的点,在坐标平面内存在点Q,使以 A、B、P、Q为顶点的四边形是菱形,
当P在y轴正半轴上,四边形ABPQ为菱形时,
①如图2所示:AQ=AB=2,且Q与A的横坐标相同,
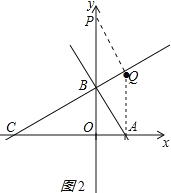
此时Q坐标为(1,2);
②如图3所示:AP=AQ=![]() ,Q与A的横坐标相同,
,Q与A的横坐标相同,
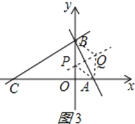
此时Q坐标为(1,![]() );
);
当P在y轴负半轴上,四边形ABPQ为菱形时,
①如图4所示:AQ=AB=2,且Q与A横坐标相同,
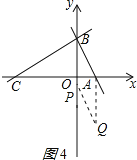
此时Q坐标为(1,-2);
②如图5所示:BP垂直平分AQ,
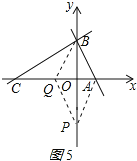
此时Q坐标为(-1,0),
综上所述:满足题意Q坐标为(1,2)、(1,-2)、(1,![]() )、(-1,0).
)、(-1,0).

【题目】为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛.为了解学生整体听写能力,赛后随机抽查了部分学生的成绩(得分取正整数,满分为100分)进行统计分析,并制作成图表:
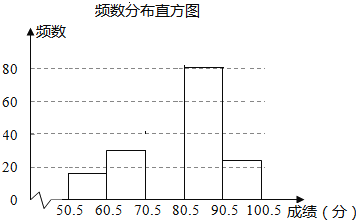
组别 | 分数段 | 频数 | 频率 |
一 | 50.5~60.5 | 16 | 0.08 |
二 | 60.5~70.5 | 30 | 0.15 |
三 | 70.5~80.5 | m | 0.25 |
四 | 80.5~90.5 | 80 | n |
五 | 90.5~100.5 | 24 | 0.12 |
请根据以上图表提供的信息,解答下列可题:
(1)这次随机抽查了______名学生,表中的数m=______,n=______;此样本中成绩的中位数落在第______组内;若绘制扇形统计图,则在修中“第三组”所对应扇形的圆心角的度数是______
(2)补全频数直方图;
(3)若成绩超过80分为优秀,请你估计该校八年级学生中汉字听写能力优秀的人数.