题目内容
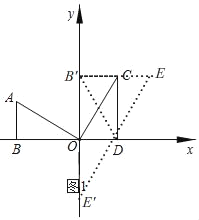
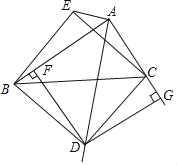
【题目】如图，两个全等的Rt△AOB、Rt△OCD分别位于第二、第一象限，∠ABO＝∠ODC＝90°，OB、OD在x轴上，且∠AOB＝30°，AB＝1．
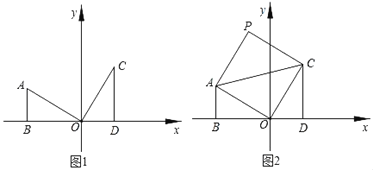
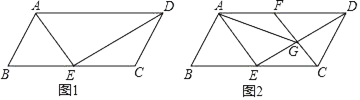
（1）如图1中Rt△OCD可以看作由Rt△AOB先绕点O顺时针旋转 度，再绕斜边中点旋转 度得到的，C点的坐标是 ；
（2）是否存在点E，使得以C、O、D、E为顶点的四边形是平行四边形，若存在，写出E点的坐标；若不存在请说明理由．
（3）如图2将△AOC沿AC翻折，O点的对应点落在P点处，求P点的坐标．
【答案】（1）90，180，（1，
）；（2）存在，E的坐标为（0，）或（2，），或（0，﹣）；（3）P（1﹣，1+）．
【解析】
(1)先求出OB,再由旋转求出OD,CD,即可得出结论;
(2)先求出D的坐标,再分三种情况,利用平行四边形的性质即可得出结论;
(3)先判断出四边形OAPC是正方形,再利用中点坐标公式即可得出结论
解：（1）Rt△OCD可以看作由Rt△AOB先绕点O顺时针旋转90°，再绕斜边中点旋转180°得到的，
在Rt△AOB中，∠AOB＝30°，AB＝1，
∴OB＝ ，
由旋转知，OD＝AB＝1，CD＝OB＝，
∴C（1，），
故答案为90，180，（1，）；
（2）存在，理由：如图1，
由（1）知，C（1，），
∴D（1，0），
∵O（0，0），
∵以C、O、D、E为顶点的四边形是平行四边形，
∴①当OC为对角线时，
∴CE∥OD，CE＝OD＝1，点E和点B'重合，
∴E（0，），
②当CD为对角线时，CE∥OD，CE＝OD＝1，
∴E（2，），
当OD为对角线时，OE'∥CD，OE'＝CD，
∴E（0，﹣），
即：满足条件的E的坐标为（0，）或（2，），或（0，﹣）；
（3）由旋转知，OA＝OC，∠OCD＝∠AOB＝30°，
∴∠COD＝90°﹣∠OCD＝60°，
∴∠AOC＝90°，
由折叠知，AP＝OA，PC＝OC，
∴四边形OAPC是正方形，
设P（m，n）
∵A（﹣，1），C（1，），O（0，0），
∴
（m+0）＝（1﹣），（n+0）＝（1+），
∴m＝1﹣，n＝1+，
∴P（1﹣，1+）．
