Question

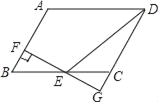
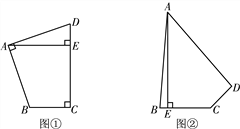
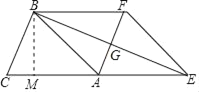
【题目】已知：如图，在△ABC中，AB＝AC＝4cm，将△ABC沿CA方向平移4cm得到△EFA，连接BE，BF；BE与AF交于点G

(1)判断BE与AF的位置关系，并说明理由；

(2)若∠BEC＝15°，求四边形BCEF的面积．

Answer 1

【答案】（1）BE⊥AF，理由详见解析；（2）12.

【解析】

（1）由△ABC沿CA方向平移4cm得到△EFA，即可得BF＝CA＝AE，AB＝EF，又由AB＝AC，证得AB＝BF＝EF＝AE，根据有四条边都相等的四边形是菱形，即可证得四边形ABFE是菱形，再根据菱形的对角线互相垂直可得BE⊥AF；

（2）首先作BM⊥AC于点M，由AB＝AE，∠BEC＝15°，求得∠BAC＝30°，那么BM＝AB＝2cm，然后利用梯形的面积公式即可求得四边形BCEF的面积．

解：（1）BE⊥AF．理由如下：

∵将△ABC沿CA方向平移4cm得到△EFA，

∴BF＝CA＝AE＝4cm，AB＝EF．

∵AB＝AC，

∴AB＝BF＝EF＝AE，

∴四边形ABFE是菱形，

∴BE⊥AF；

（2）作BM⊥AC于点M．

∵AB＝AE，∠BEC＝15°，

∴∠ABE＝∠AEB＝15°，

∴∠BAC＝30°．

∴BM＝AB＝2cm．

∵BF＝CA＝AE＝4cm，

∴四边形BCEF的面积＝（BF+CE）BM

＝×12×2

＝12．