题目内容
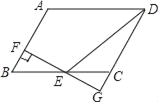
【题目】如图,含45°角的直角三角板DBC的直角顶点D在∠BAC的角平分线AD上,DF⊥AB于F,DG⊥AC于G,将△DBC沿BC翻转,D的对应点落在E点处,当∠BAC=90°,AB=4,AC=3时,△ACE的面积等于_____.
【答案】![]()
【解析】
根据勾股定理得到BC=5,由折叠的性质得到△BCE是等腰直角三角形,过E作EH⊥AC交CA的延长线于H,根据勾股定理得到EH=![]() ,于是得到结论
,于是得到结论
∵在△ABC中,∠BAC=90°,AB=4,AC=3,
∴BC=5,
∵△BCE是△DBC沿BC翻转得到得
∴△BCE是等腰直角三角形,
∴∠BEC=90°,∠BCE=45°,CE=![]() ,BC=
,BC=![]()
过E作EH⊥AC交CA的延长线于H,
易证△CEH≌△DCG,△DBF≌△DCG
∴EH=CG, BF=CG,
∵四边形AFDG和四边形BECD是正方形
∴AF=AG,
设BF=CG=x,则AF=4-x,AG=3+x
∴4-x=3+x,
∴x=![]()
∴EH=CG=![]()
∴△ACE的面积=![]() ×
×![]() ×3=
×3=![]() ,
,
故答案为: ![]()

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 | 80 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 | 85 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分).
(1)这6名选手笔试成绩的中位数是________分,众数是________分;
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.