题目内容
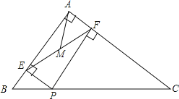
【题目】如图,平行四边形ABCD中,AE、DE分别平分∠BAD、∠ADC,E点在BC上.
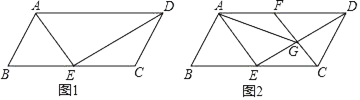
(1)求证:BC=2AB;
(2)若AB=3cm,∠B=60°,一动点F以1cm/s的速度从A点出发,沿线段AD运动,CF交DE于G,当CF∥AE时:
①求点F的运动时间t的值;②求线段AG的长度.
【答案】(1)见解析;(2)①t=3(秒);②AG=![]() .
.
【解析】
(1)先判断出∠DAE=∠AEB,再判断出∠DAE=∠BAE,进而得出∠BAE=∠AEB,即可判断出AB=BE同理:判断出CE=AB,即可得出结论
(2)①先判断出四边形AECF是平行四边形,进而求AF=3,即可得出结论
②先判断出△ABE是等边三角形,进而求出∠AEB=60°,AE=3cm,再判断出∠DCF=∠ECF,即可判断出∠CGE=90°,最后用勾股定理即可得出结论.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠DAE=∠AEB,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=BE,
同理:CE=CD,
∴BE=CE=AB,
∴BC=BE+CD=2AB;
(2)①由(1)知,CE=CD=AB,
∵AB=3cm,
∴CE=3cm,
∵四边形ABCD是平行四边形,
∴AD∥BC
∵AE∥CF,
∴四边形AECF是平行四边形,
∴AF=CE=3cm,
∴点F的运动时间t=3÷1=3(秒);
②由(1)知AB=BE,
∵∠B=60°,
∴△ABE是等边三角形,
∴∠AEB=60°,AE=AB=3cm,
∵四边形ABCD是平行四边形,
∴∠B+∠BCD=180°,
∵∠B=60°,
∴∠BCD=120°,
∵AE∥CF,
∴∠ECF=∠AEB=60°,
∴∠DCF=∠BCD﹣∠ECF=60°=∠ECF,
由(1)知,CE=CD=AB=3cm,
∴CF⊥DE,
∴∠CGE=90°,
在Rt△CGE中,∠CEG=90°﹣∠ECF=30°,CG=![]() CE=
CE=![]() ,
,
∴EG=![]() CG=
CG=![]() ,
,
∵∠AEB=60°,∠CEG=30°,
∴∠AEG=90°,
在Rt△AEG中,AE=3,根据勾股定理得,AG=![]() .
.